河南省三门峡义马市2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2021-09-16 类型：期中考试

进入出卷网下载

一、单选题

1. 下列说法正确的是（）.

A、-1是最大的负数 B、两个数的和一定大于其中的任意一个数 C、两个数的差一定小于被减数 D、所有的有理数都能用数轴上的点表示

查看试题解析
2. 有如下一些数：-3，-3.14， $- (- 20)$ ，0，+2.1， $- \frac{1}{3}$ ， $| - 9 |$ ；其中负数有（）.

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积相当于35个标准足球场的总面积．已知每个标准足球场的面积为 $7140 m^{2}$ ，则FAST的反射面积总面积约为（）

A、 $7.14 \times 10^{3} m^{2}$ B、 $7.14 \times 10^{4} m^{2}$ C、 $2.5 \times 10^{5} m^{2}$ D、 $2.5 \times 10^{6} m^{2}$

查看试题解析
4. 计算 $\frac{1}{1 \times 2} - \frac{1}{2 \times 3} - \frac{1}{3 \times 4} - \frac{1}{4 \times 5} - \frac{1}{5 \times 6} - \frac{1}{6 \times 7}$ 的结果为（）.

A、 $\frac{6}{7}$ B、 $- \frac{6}{7}$ C、 $- \frac{1}{7}$ D、 $\frac{1}{7}$

查看试题解析
5. 已知有理数 $a$ ， $b$ 在数轴上的位置如图所示，则 $a$ ， $- b$ ， $- a$ ， $b$ 从大到小的顺序为（）.

A、 $b > a > - a > - b$ B、 $- a > - b > a > b$ C、 $b > - a > a > - b$ D、 $- a > a > - b > b$

查看试题解析
6. 如果a+b>0，且ab>0，那么（）

A、a>0，b>0 B、a<0，b<0 C、a、b异号且正数的绝对值较小 D、a、b异号且负数的绝对值较小

查看试题解析
7. 用式子表示“比a的2倍大1的数”是（）．

A、 $2 (a + 1)$ B、 $2 (a - 1)$ C、 $2 a + 1$ D、 $2 a - 1$

查看试题解析
8. 下列说法正确的是（　　）

A、﹣ $\frac{2 x y}{5}$ 的系数是﹣2 B、x²+x﹣1的常数项为1 C、2²ab³的次数是6次 D、2x﹣5x²+7是二次三项式

查看试题解析
9. 已知代数式x-2y的值是3，则代数式 $1 - x + 2 y$ 的值是（）

A、-2 B、2 C、4 D、-4

查看试题解析
10. 某粮店出售的三种品牌的面粉袋上，分别标有质量为（25±0.1）kg，（25±0.2）kg，（25±0.3）kg的字样，从中任意拿出两袋，它们的质量最多相差（　　）

A、0.8kg B、0.6kg C、0.5kg D、0.4kg

查看试题解析

二、填空题

11. $- \frac{2}{3}$ 的绝对值是．

查看试题解析
12. ﹣a的相反数是.﹣a的相反数是﹣5，则a=.

查看试题解析
13. 若x^my²和x³yⁿ是同类项，则mⁿ＝.

查看试题解析
14. 若关于 $x$ ， $y$ 的式子 $m x^{3} - 3 n x y^{2} + 2 x^{3} - x y^{2} + y$ 中不含三次项，则 ${(m - 3 n)}^{2020} =$ .

查看试题解析
15. 已知 $m$ ， $n$ 为有理数，且 $m \neq 0$ ， $n > 0$ ，则 $\frac{| m |}{m} + \frac{| n |}{n} + \frac{| m n |}{m n}$ 的值是.

查看试题解析

三、解答题

16. 计算：

(1)、 $4 \frac{3}{4} - (+ 3.85) - (- 3 \frac{1}{4}) + (- 3.15)$

(2)、 $- 3^{2} - 1^{4} - \frac{1}{6} \times [3 - {(- 3)}^{2}]$

查看试题解析
17. 先化简，再求值： $(5 a^{2} + 2 a - 1) - 4 (3 - 8 a + 2 a^{2})$ ，其中a是最大的负整数．

查看试题解析
18. 点A、B在数轴上的位置如图所示：

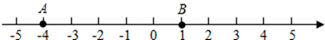(1)、点A表示的数是，点B表示的数是；

(2)、在原图中分别标出表示 $+ 3$ 的点C、表示 $- 1.5$ 的点D；

(3)、在上述条件下，B、C两点间的距离是，A、C两点间的距离是

查看试题解析
19. 某登山队以二号营地为基准，开始向距二号营地500米的顶峰冲击，他们记向上为正，行进过程记录如下：（单位：米）： +150， -35， -40，+210，-32， +20， -18， -5， +20， +85，-25．

(1)、他们最终有没有登上顶峰?若没有，距顶峰还有多少米?

(2)、登山时，若5名队员在记录的行进路线上都使用了氧气，且每人每米要消耗氧气0.04升，则他们共耗氧多少升?

查看试题解析
20. 已知 $a$ ， $b$ 互为相反数， $c$ ， $d$ 互为倒数， $m$ 的绝对值是2，求 $| a + b | + 2 m^{2} + 4 m - 3 c d$ 的值.

查看试题解析
21. 已知 $A = x^{2} + 3 x y - 12$ ， $B = 2 x^{2} - x y + y$ .

(1)、当 $x = y = - 2$ 时，求 $2 A - B$ 的值；

(2)、若 $2 A - B$ 的值与 $y$ 的取值无关，求 $x$ 的值.

查看试题解析
22.
在沙坪坝住房小区建设中，为了提高业主的宜居环境，某小区规划修建一个广场（平面图形如图所示）

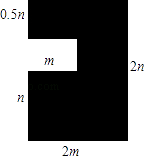(1)、用含m，n的代数式表示该广场的面积S；

(2)、若m，n满足（m﹣6）²+|n﹣5|=0，求出该广场的面积．

查看试题解析
23. 先阅读下列材料，然后解答问题：
材料 1：从三张不同的卡片中选出两张排成一列，有6种不同的排法，抽象成数学问题就是从3个不同的元素中选取2个元素的排列，排列记为 $A_{3}^{2}$ =3×2=6.

一般地，从 n 个不同的元素中选取 m 个元素的排列数记作 $A_{n}^{m}$ =n（n﹣1）（n﹣2）（n﹣3）…（n﹣m+1）（m≤n）

例：从5个不同的元素中选取3个元素排成一列的排列数为： $A_{5}^{3}$ =5×4×3=60.

材料 2：从三张不同的卡片中选取两张，有3种不同的选法，抽象成数学问题就

是从3个元素中选取2个元素的组合，组合数为 $C_{3}^{2} = \frac{3 \times 2}{2 \times 1} = 3$ .

一般地，从n个不同元素中选取m个元素的组合数记作 $C_{n}^{m}$ ， $C_{n}^{m} = \frac{n (n - 1) ... (n - m + 1)}{m (m - 1) ... \times 2 \times 1}$ （m≤n）

例：从6个不同的元素选3个元素的组合数为： $C_{6}^{3} = \frac{6 \times 5 \times 4}{3 \times 2 \times 1} = 20$ .

问：

(1)、从某个学习小组8人中选取3人参加活动，有种不同的选法；

(2)、从7个人中选取4人，排成一列，有种不同的排法.

查看试题解析