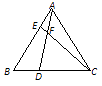初中数学湘教版八年级上册第二章三角形单元检测
试卷更新日期:2021-09-15 类型:单元试卷
一、单选题
-
1. 三角形一边上的中线把原三角形一定分成两个( )A、形状相同的三角形 B、面积相等的三角形 C、直角三角形 D、周长相等的三角形2. 下列长度的三条线段能组成三角形的是( )A、1,2,3 B、3,4,5 C、3,1,1 D、3,4,73. 用反证法证明“在直角三角形中,至少有一个锐角不大于45º”,应先假设这个直角三角形中( )A、有一个锐角小于45º B、每一个锐角都小于45º C、有一个锐角大于45º D、每一个锐角都大于45º4. 下列命题的逆命题是真命题的是( )A、如果a>0,b>0,则a+b>0 B、直角都相等 C、两直线平行,同位角相等 D、若a=b,则|a|=|b|5. 等腰三角形的一个角是48°,它的一个底角的度数是( )A、48° B、48°或42° C、42°或66° D、48°或66°6. 在如图的网格上,能找出几个格点,使每一个格点与A,B两点能构成的等腰三角形个数为( )
 A、3个 B、4个 C、5个 D、6个7. 如图,在△ABE中,AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠BAE的度数是( )
A、3个 B、4个 C、5个 D、6个7. 如图,在△ABE中,AE的垂直平分线MN交BE于点C,∠E=30°,且AB=CE,则∠BAE的度数是( )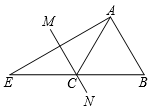 A、80° B、85° C、90° D、105°8. 在联欢晚会上,有A,B,C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在△ABC的( )A、三边中线的交点 B、三边垂直平分线的交点 C、三边上高的交点 D、三条角平分线的交点9. 下面各条件中,能使△ABC≌△DEF的条件是( )A、AB=DE,∠A=∠D,BC=EF B、AB=BC,∠B=∠E,DE=EF C、AB=EF,∠A=∠D,AC=DF D、BC=EF,∠C=∠F,AC=DF10. 如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则
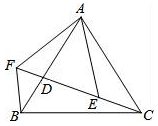
A、80° B、85° C、90° D、105°8. 在联欢晚会上,有A,B,C三名同学站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置在△ABC的( )A、三边中线的交点 B、三边垂直平分线的交点 C、三边上高的交点 D、三条角平分线的交点9. 下面各条件中,能使△ABC≌△DEF的条件是( )A、AB=DE,∠A=∠D,BC=EF B、AB=BC,∠B=∠E,DE=EF C、AB=EF,∠A=∠D,AC=DF D、BC=EF,∠C=∠F,AC=DF10. 如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则下列结论,其中正确的是( )
①△AFB≌△AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC.
 A、①②③ B、①②④ C、①② D、①②③④
A、①②③ B、①②④ C、①② D、①②③④二、填空题
-
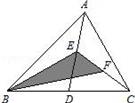
11. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且△ABC的面积等于4cm2 , 则阴影部分图形面积等于cm2
 12. 用反证法证明“a>b”时,首先应该假设 .
12. 用反证法证明“a>b”时,首先应该假设 .
13. 等腰三角形一腰上的高与另一腰的夹角为50°,则它的底角等于。14. 如图,在△ABC中,∠C=90°,点E是AC上的点,且∠1=∠2,DE垂直平分AB,垂足是D,如果EC=3cm,则AE等于 .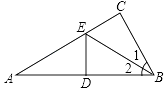 15. 如图由6个边长等的正方形的组合图形,则∠1+∠2+∠3= .
15. 如图由6个边长等的正方形的组合图形,则∠1+∠2+∠3= .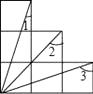 16. 人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:
16. 人教版初中数学教科书八年级上册第35-36页告诉我们作一个三角形与已知三角形全等的方法:已知: .
求作: ,使得 ≌ .
作法:如图.
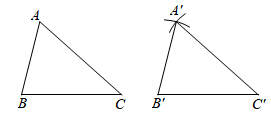
( 1 )画 ;
( 2 )分别以点 , 为圆心,线段 , 长为半径画弧,两弧相交于点 ;
( 3 )连接线段 , ,则 即为所求作的三角形.
请你根据以上材料完成下列问题:
(1)、完成下面证明过程(将正确答案填在相应的横线上):证明:由作图可知,在 和 中,
∴ ≌_▲_.
(2)、这种作一个三角形与已知三角形全等的方法的依据是.(填序号)①AAS;②ASA;③SAS;④SSS
三、作图题
-
17. 已知:∠α,直线l及l上两点A,B.求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α.
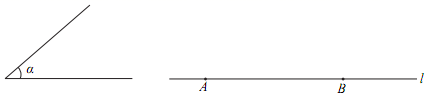 18. 如图,已知线段 和 ,求作一个等腰三角形,使它的腰长等于 ,底边长等于 .(温馨提示:不写作法,只保留作图痕迹)
18. 如图,已知线段 和 ,求作一个等腰三角形,使它的腰长等于 ,底边长等于 .(温馨提示:不写作法,只保留作图痕迹)
四、解答题
-
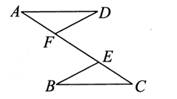
19. 如图,AE=CF,AD=CB,DF=BE,求证:△ADF≌△CBE。
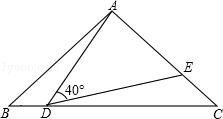
 20. 如图所示,在△ABC中,D是BC边上一点∠1=∠2,∠3=∠4,∠BAC=69°,求∠DAC的度数.
20. 如图所示,在△ABC中,D是BC边上一点∠1=∠2,∠3=∠4,∠BAC=69°,求∠DAC的度数.
五、综合题