吉林省吉林市舒兰市2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-09-15 类型：期末考试

进入出卷网下载

一、单选题

1. 比－1小的数是（）.

A、0 B、－ $\frac{1}{2}$ C、－2 D、1

查看试题解析
2. 检测4个排球，其中超过标准的克数记为正数，低于标准的克数记为负数，从轻重的角度来看，最接近标准的球是（）

A、 B、 C、 D、

查看试题解析
3. 如图，在数轴上点P表示的数可能是（）

A、-2.3 B、-1.7 C、-0.3 D、0.3

查看试题解析
4. 下列图形中，可以是正方体展开图的是（）

A、 B、 C、 D、

查看试题解析
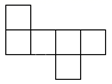5. 某商店换季促销，将一件标价为240元的T恤8折售出，获利20%，则这件T恤的成本为（）

A、144元 B、160元 C、192元 D、200元

查看试题解析
6. 已知实数a，b在数轴上对应点的位置如图所示，则下列判断错误的是（）

A、a<1 B、b-a>0 C、ab>0 D、1-b<0

查看试题解析
7. 如图，一副三角板（直角顶点重合）摆放在桌面上，若∠AOD＝150°，则∠BOC等于（）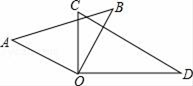

A、30° B、45° C、50° D、60°

查看试题解析
8. 有下列四种说法：①锐角的补角一定是钝角；②一个角的补角一定大于这个角；③如果两个角是同一个角的补角，那么它们相等；④锐角和钝角互补．其中正确的是（）

A、①② B、①③ C、①②③ D、①②③④

查看试题解析

二、填空题

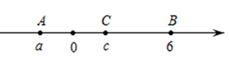
9. 要在墙壁上固定一根小木条，至少需要两枚钉子，其数学原理是.

查看试题解析
10. 火星和地球的最近距离约为55000000千米，用科学记数法表示55000000的结果是千米．

查看试题解析
11. 比较大小： $- \frac{3}{7}$ $- \frac{8}{21}$

查看试题解析
12. 若单项式 $- \frac{2 x^{2} y}{3}$ 的系数是 $m$ ，次数是 $n$ ，则 $m n =$ .

查看试题解析
13. 如图，数轴上A，B，C三点所表示的数分别是a，6，c，已知AB=8，a+c=0，则c的值为．

查看试题解析
14. 一个角的余角是 $54^{\circ} 4 0^{'}$ ，则这个角的补角是.

查看试题解析
15. 如图1，将一个边长为 $a$ 的正方形纸片剪去两个小矩形，得到一个“ ”的图案，如图2所示，再将剪下的两个小矩形拼成一个新的矩形，如图3所示，则新矩形的周长为.

查看试题解析
16. 我们定义： $| \begin{matrix} a & b \\ c & d \end{matrix} | = a d - b c$ ，例如： $| \begin{matrix} 2 & 3 \\ 4 & 5 \end{matrix} | = 2 \times 5 - 3 \times 4 = - 2$ .若 $| \begin{matrix} 3 x & 7 \\ x - 1 & 1 \end{matrix} | = 0$ ，则 $x$ 的值为.

查看试题解析

三、解答题

17. 计算： $- 1^{2} - 6 \div (- 2) \times | - \frac{1}{3} |$

查看试题解析
18. 如图，在平面内有A，B，C三点，按要求画图：
⑴画线段AC；

⑵画射线BC；

⑶画直线AB．

查看试题解析
19. 已知下面5个式子：① x²-x+1，② m²n+mn-1，③ $x^{4} + \frac{1}{x} + 2$ ， ④ 5-x² ， ⑤ -x² ．回答下列问题：

(1)、上面5个式子中有个多项式，次数最高的多项式为（填序号）；

(2)、选择2个二次多项式，并进行加法运算．

查看试题解析
20. 解方程： $\frac{x + 1}{2} - 3 = \frac{2 - x}{4}$

查看试题解析
21. 如图①，已知 $A B = 6 ， B C = 4$ ，点 $D$ 为 $A C$ 的中点.

(1)、求线段 $B D$ 的长；

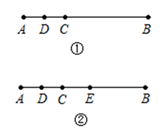(2)、若点 $E$ 为图①中线段 $B C$ 的一个三等分点（点 $E$ 靠近点 $C$ ，如图②），直接写出线段 $A E$ 的长.

查看试题解析
22. 如图，已知轮船A在灯塔P的北偏东30°的方向上，轮船B在灯塔P的南偏东70°的方向上．

(1)、求从灯塔P看两轮船的视角（即∠APB）的度数？

(2)、轮船C在∠APB的角平分线上，则轮船C在灯塔P的什么方位？

查看试题解析
23. 如图，四边形ABCD和ECGF都是正方形.

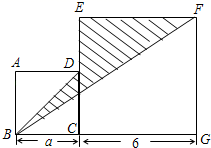(1)、用代数式表示阴影部分的面积；（结果要求化简）

(2)、当a＝4时，求阴影部分的面积.

查看试题解析
24. 某丝巾厂家70名工人义务承接了2020年上海进博会上志愿者佩戴的手环、丝巾的制作任务．已知每人每天平均生产手环180个或者丝巾120条，一条丝巾要配两个手环．

(1)、为了使每天生产的丝巾和手环刚好配套，应分配多少名工人生产手环，多少名工人生产丝巾？

(2)、在（1）的方案中，能配成套．

查看试题解析
25. 直角三角板ABC的直角顶点C在直线DE上，CF平分∠BCD．

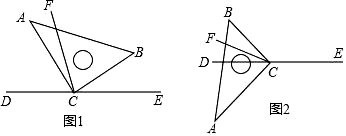(1)、在图1中，若∠BCE=40°，求∠ACF的度数；

(2)、在图1中，若∠BCE=α，直接写出∠ACF的度数（用含α的式子表示）；

(3)、将图1中的三角板ABC绕顶点C旋转至图2的位置，探究：写出∠ACF与∠BCE的度数之间的关系，并说明理由．

查看试题解析
26. 如图，数轴上 $A ， B$ 两点开始时所对应的数分别是 $- 12$ 和6. $A ， B$ 两点各自以一定的速度在数轴上运动，且 $A$ 点的运动速度为2个单位长度∕秒.

(1)、若点 $P$ 为 $A ， B$ 两点初始时线段 $A B$ 的中点，则点 $P$ 所表示的数是；

(2)、 $A ， B$ 两点同时出发相向而行，在原点处相遇，求 $B$ 点的运动速度；

(3)、若 $A ， B$ 两点按（2）中的速度同时出发，向数轴正方向运动，几秒时两点相距6个单位长度？

查看试题解析