广东省汕头市龙湖区2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-09-15 类型:期末考试
一、单选题
-
1. 中国人很早就开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入了负数.如果支出150元记作-150元,那么+80元表示( )
 A、收入80元 B、支出80元 C、收入20元 D、支出20元2. 下列方程中,是一元一次方程的是A、 B、 C、 D、3. 下列各式中运算正确的是( )A、 B、 C、 D、4. 把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释正确的是( )A、线段可以比较大小 B、线段有两个端点 C、两点之间线段最短 D、过两点有且只有一条直线5. 把下图折成正方体的盒子,折好后与“试”相对的字是( )
A、收入80元 B、支出80元 C、收入20元 D、支出20元2. 下列方程中,是一元一次方程的是A、 B、 C、 D、3. 下列各式中运算正确的是( )A、 B、 C、 D、4. 把一条弯曲的公路改成直道,可以缩短路程,其道理用几何知识解释正确的是( )A、线段可以比较大小 B、线段有两个端点 C、两点之间线段最短 D、过两点有且只有一条直线5. 把下图折成正方体的盒子,折好后与“试”相对的字是( ) A、祝 B、你 C、顺 D、利6. 一小袋味精的质量标准为“ 克”,那么下列四小袋味精质量符合要求的是( )A、50.35克 B、49.80克 C、49.72克 D、50.40克7. 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
A、祝 B、你 C、顺 D、利6. 一小袋味精的质量标准为“ 克”,那么下列四小袋味精质量符合要求的是( )A、50.35克 B、49.80克 C、49.72克 D、50.40克7. 实数a,b在数轴上的位置如图所示,以下说法正确的是( ) A、a+b=0 B、b<a C、ab>0 D、|b|<|a|8. 将一副三角尺按不同位置摆放,摆放方式中∠α 与∠β 互余的是( )A、
A、a+b=0 B、b<a C、ab>0 D、|b|<|a|8. 将一副三角尺按不同位置摆放,摆放方式中∠α 与∠β 互余的是( )A、 B、
B、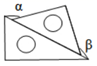 C、
C、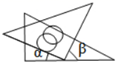 D、
D、 9. 下列说法中正确的个数为( )
9. 下列说法中正确的个数为( )⑴正数与负数互为相反数;⑵单项式 的系数是3,次数是2;
⑶如果 ,那么 ;⑷过两点有且只有一条直线;
⑸一个数和它的相反数可能相等;⑹射线比直线小一半.
A、1个 B、2个 C、3个 D、4个10. 观察下面由正整数组成的数阵:
照此规律,按从上到下、从左到右的顺序,第51行的第1个数是( )
A、2500 B、2501 C、2601 D、2602二、填空题
-
11. 中国在第二十三届冬奥会闭幕式上奉献了《2022相约北京》的文艺表演,会后表演视频在网络上推出,即刻转发量就超过810000,这个数用科学记数法表示为12. 比较大小: (填“<”、“=”或“>”)13. 用四舍五入法按要求取近似值: (精确到千分位).14. 若 是同类项,则 .15. 若 是关于x的方程 的解,则m的值为 .16. 已知 与 互余,且 ,则 为°.17. 在数轴上,点O为原点,点 分别表示数 ,现将点A向右平移2个单位长度得到点C,若 ,则 的值为 .
三、解答题
-
18. 如图,已知平面上三点 ,请按要求完成:
⑴画射线 ,直线 ;
⑵连接 ,并用圆规在线段 的延长线上截取 ,连接 (保留画图痕迹).
 19. 计算:20. 解方程:21. 如图,已知线段AB=4,延长线段AB到C,使BC=2AB.
19. 计算:20. 解方程:21. 如图,已知线段AB=4,延长线段AB到C,使BC=2AB.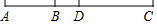 (1)、求线段AC的长;(2)、若点D是AC的中点,求线段BD的长.22. 一个长方形养鸡场的长边靠墙,墙长 ,其他三边用竹篱笆围成,现有长为 的竹篱笆,小林打算用它围成一个鸡场,其中长比宽多 ;小陈也打算用它围成一个鸡场,其中长比宽多 .(1)、你认为谁的设计符合实际?通过计算说明理由.(2)、在(1)的条件下,按照设计鸡场面积是 .(直接在横线填上答案)23. 先化简,再求值:
(1)、求线段AC的长;(2)、若点D是AC的中点,求线段BD的长.22. 一个长方形养鸡场的长边靠墙,墙长 ,其他三边用竹篱笆围成,现有长为 的竹篱笆,小林打算用它围成一个鸡场,其中长比宽多 ;小陈也打算用它围成一个鸡场,其中长比宽多 .(1)、你认为谁的设计符合实际?通过计算说明理由.(2)、在(1)的条件下,按照设计鸡场面积是 .(直接在横线填上答案)23. 先化简,再求值:,其中 的值满足 .
24. 为发展校园足球运动,某城区四校决定联合购买一批足球运动装备.市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.(1)、求每套队服和每个足球的价格是多少元;(2)、若城区四校联合购买100套队服和a(a>10)个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花发费用;(3)、在(2)的条件下,假如你是本次购买任务的负责人,你认为到甲、乙哪家商场购买比较合算?25. 探索新知:
如图1,射线 在 的内部,图中共有3个角: 和 ,若其中有一个角的度数是另一个角度数的两倍,则称射线 是 的“巧分线”
(1)、一个角的平分线这个角的“巧分线”(填“是”或“不是”);(2)、如图2,若 ,且射线 是 的“巧分线”,则 ;(用含 的代数式表示);(3)、如图2,若 ,且射线 绕点P从 位置开始,以每秒 的速度逆时针旋转,当 与 成 时停止旋转,旋转的时间为t秒.若射线 同时绕点P以每秒 的速度逆时针旋转,并与 同时停止,请求出当射线 是 的“巧分线”时的值.