广东省惠州市惠东县2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-09-15 类型:期末考试
一、单选题
-
1. 有理数 的倒数为( )A、 B、 C、 D、2. 2019年11月1日,隆生大桥正式通车,缓解了东江大桥与中信大桥的交通压力,其特点是“直”,明显缩短了江北与水口的距离,其主要依据是( )
 A、两点确定一条直线 B、过一点有且只有一条直线与已知直线垂直 C、垂线段最短 D、两点之间,线段最短3. 下列等式变形正确的是( )A、若﹣3x=5,则x= B、若 ,则2x+3(x﹣1)=1 C、若5x﹣6=2x+8,则5x+2x=8+6 D、若3(x+1)﹣2x=1,则3x+3﹣2x=14. 有理数 在数轴上的位置如图所示,则化简 的结果为( )
A、两点确定一条直线 B、过一点有且只有一条直线与已知直线垂直 C、垂线段最短 D、两点之间,线段最短3. 下列等式变形正确的是( )A、若﹣3x=5,则x= B、若 ,则2x+3(x﹣1)=1 C、若5x﹣6=2x+8,则5x+2x=8+6 D、若3(x+1)﹣2x=1,则3x+3﹣2x=14. 有理数 在数轴上的位置如图所示,则化简 的结果为( ) A、 B、 C、 D、5. 若 是关于 的一元一次方程,则 的值是( )A、1 B、2 C、3 D、46. 若方程2x+a﹣14=0的解是x=﹣2,则a的值为( )A、10 B、7 C、18 D、﹣187. 2020年春节前夕,一场突如其来的新冠肺炎疫情牵动着全国人民的心,因疫情发展迅速,全国口罩防护用品销售量暴涨、供应紧张,国有疫,我有责,在特殊时期,某集团紧急启动了应急响应机制,取消了工人休假,与防疫救灾相关的口罩,84消毒液生产线连续24小时运转,将援驰武汉的10万片口罩,5万瓶84消毒液和201万片酒精棉片第一时间发往武汉,其中201万用科学记数法表示为( )A、 B、 C、 D、8. 已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是( )A、﹣5x﹣1 B、5x+1 C、﹣13x﹣1 D、13x+19. 一件标价为200元的商品,若该商品按九折销售,则该商品的实际售价是( )A、200 B、180 C、90 D、2010. 过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其符合题意展开图正确的为( )
A、 B、 C、 D、5. 若 是关于 的一元一次方程,则 的值是( )A、1 B、2 C、3 D、46. 若方程2x+a﹣14=0的解是x=﹣2,则a的值为( )A、10 B、7 C、18 D、﹣187. 2020年春节前夕,一场突如其来的新冠肺炎疫情牵动着全国人民的心,因疫情发展迅速,全国口罩防护用品销售量暴涨、供应紧张,国有疫,我有责,在特殊时期,某集团紧急启动了应急响应机制,取消了工人休假,与防疫救灾相关的口罩,84消毒液生产线连续24小时运转,将援驰武汉的10万片口罩,5万瓶84消毒液和201万片酒精棉片第一时间发往武汉,其中201万用科学记数法表示为( )A、 B、 C、 D、8. 已知一个多项式与3x2+9x的和等于3x2+4x﹣1,则这个多项式是( )A、﹣5x﹣1 B、5x+1 C、﹣13x﹣1 D、13x+19. 一件标价为200元的商品,若该商品按九折销售,则该商品的实际售价是( )A、200 B、180 C、90 D、2010. 过正方体中有公共顶点的三条棱的中点切出一个平面,形成如图几何体,其符合题意展开图正确的为( )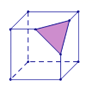 A、
A、 B、
B、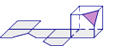 C、
C、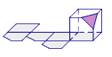 D、
D、
二、填空题
-
11. 在我校第8届校运会的跳远比赛中,以4.00米为标准,若小明跳出了4.22米,可记作+0.22,那么小东跳出了3.85米,记作 .12. 若单项式 与 的和仍是单项式,则 .13. 若 和 互为相反数, 和 互为倒数,则 的值是 .14. 一个角的补角比它的余角的3倍还多10°,则这个角的度数为 .15. 如图,过直线AB上一点O作射线OC,∠BOC=29°18′,则∠AOC的度数为 .
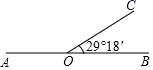 16. 如图,将一副三角板叠在一起,使它们的直角顶点重合于O点,且∠AOB=155°,则∠COD= .
16. 如图,将一副三角板叠在一起,使它们的直角顶点重合于O点,且∠AOB=155°,则∠COD= .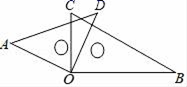 17. 观察下列等式:
17. 观察下列等式:……
请按上述规律,写出第 个式子的计算结果( 为正整数) . (写出最简计算结果即可)
三、解答题
-
18. 计算:19. 先化简,再求值: ,其中 , .20. 解方程:21. 一艘船从甲码头到乙码头顺流行驶,用了2h;从乙码头返回甲码头,逆流行驶,用了2.5h,已知水流的速度是3km/h,求船在静水中的速度?甲,乙两码头之间的距离?22. 已知如图, 平分 , 平分 ,
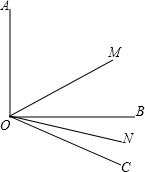 (1)、若 ,求 ;(2)、若 ,其他条件不变,求 .23. 在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:
(1)、若 ,求 ;(2)、若 ,其他条件不变,求 .23. 在“节能减排,做环保小卫士”活动中,小明对两种照明灯的使用情况进行了调查,得出如表所示的数据:功率
使用寿命
价格
普通白炽灯
100瓦(即0.1千瓦)
2000小时
3元/盏
优质节能灯
20瓦(即0.02千瓦)
4000小时
35元/盏
已知这两种灯的照明效果一样,小明家所在地的电价是每度0.5元.
(注:用电度数=功率(千瓦)×时间(小时),费用=灯的售价+电费)
请解决以下问题:
(1)、在白炽灯的使用寿命内,设照明时间为x小时,请用含x的代数式分别表示用一盏白炽灯的费用y1(元)和一盏节能灯的费用y2(元):(2)、在白炽灯的使用寿命内,照明多少小时时,使用这两种灯的费用相等?(3)、如果计划照明4000小时,购买哪一种灯更省钱?请你通过计算说明理由.24. 如图1, 点从点 开始以2厘米/秒的速度沿 的方向移动,点 从点 开始以1厘米/秒的速度沿 的方向移动,当 点到达 点时, 、 两点都停止运动:在直角三角形 中, ,若 厘米, 厘米, 厘米,如果点 、 同时出发,用 (秒)表示移动时间,那么:(1)、如图1,若点 在线段 上运动,点 在线段 上运动,试求出 为何值时, .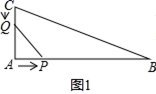 (2)、如图2,点 在 上运动,试求出 为何值时,三角形 的面积等于三角形 面积的 ;
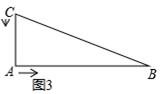
(2)、如图2,点 在 上运动,试求出 为何值时,三角形 的面积等于三角形 面积的 ; (3)、如图3,试求当 为何值时,线段 的长度等于线段 的长度的 .
(3)、如图3,试求当 为何值时,线段 的长度等于线段 的长度的 .