广东省佛山市禅城区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-09-15 类型：期末考试

进入出卷网下载

一、单选题

1. $- 2$ 的相反数是（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. “全民行动，共同节约”，我国14亿人口如果都响应国家号召每人每年节约1度电，一年可节的1400000000度，这个数用科学记数法表示，正确的是（）

A、 $14 \times 10^{8}$ B、 $1.4 \times 10^{9}$ C、 $0.14 \times 10^{10}$ D、 $1.4 \times 10^{10}$

查看试题解析
3. 下图是由四个相同的小正方体搭成的一个几何体，从左面看到的几何体的形状图是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式计算正确的是（）

A、 $- m - m = 0$ B、 $- a + a = 0$ C、 $- (a + 1) = - a + 1$ D、 $- 2^{2} = {(- 2)}^{2}$

查看试题解析
5. 在完成“创文”黑板报的时候，101班的宣传小组先在黑板上画出两个点，然后过这两点弹出一条墨线，这是因为（）

A、两点之间，线段最短 B、过一点，有无数条直线 C、两点确定一条直线 D、两点之间线段的长度叫做两点之间的距离

查看试题解析
6. 下列关于单项式 $- \frac{2 x^{2} y}{3}$ 的说法中，正确的是（）

A、系数是2，次数是2 B、系数是 $- 2$ ，次数是3 C、系数是 $- \frac{2}{3}$ ，次数是2 D、系数是 $- \frac{2}{3}$ ，次数是3

查看试题解析
7. 下列调查中，最适合采用普查方式的是（）

A、调查某种灯泡的使用寿命 B、调查某学校七年级（1）班学生对篮球的爱好情况 C、调查全国中学生的节水情况 D、调查我国八年级学生的视力情况

查看试题解析
8. 数 $a$ 和数 $b$ 在数轴上的位置如图，化简 $| a - b |$ 的结果是（）

A、a-b B、 $b - a$ C、 $- a - b$ D、a+b

查看试题解析
9. “喜茶”店中的A种奶茶比B种奶茶每杯贵5元，小颖买了3杯A种奶茶、5杯B种奶茶，一共花了135元，问A种奶茶、B种奶茶每杯分别的多少元？若设A种奶茶 $x$ 元，则下列方程中正确的是（）

A、 $5 x + 3 (x - 5) = 135$ B、 $5 (x - 5) + 3 x = 135$ C、 $5 x + 3 (x + 5) = 135$ D、 $5 (x + 5) + 3 x = 135$

查看试题解析
10. 观察下面“品”字形中各数之间的规律，根据观察到的规律得出a+b的值为（）

A、32 B、33 C、34 D、35

查看试题解析

二、填空题

11. 如果零上2℃记作+2℃，那么零下3℃记作℃．

查看试题解析
12. 角度单位换算： $1.4 ° =$ ′．

查看试题解析
13. “垃圾分类”知识竞赛规定：答对的得10分，答错或不答扣5分，如果初一（2）班答对了 $a$ 道题，答错了 $b$ 道题，那么初一（2）班的得分可以表示为：分．

查看试题解析
14. 如果 $x = 1$ 是关于 $x$ 的方程 $5 x + 2 m = 7$ 的解，那么 $m$ 的值是．

查看试题解析
15. 如图所示是一个运算程序，若输入的值为－2，则输出的结果为．

查看试题解析
16. 已知如图， $∠ A O B$ 和 $∠ C O D$ 都是直角， $∠ A O D = 25 °$ ．下列结论正确的是（只填序号）．
① $∠ A O C = 75 °$ ．② $∠ A O C = ∠ B O D$ ．③ $∠ B O C = 90 ° + ∠ B O D$ ．④ $∠ B O C = 155 °$ ；

查看试题解析
17. 点 $C$ 在直线 $A B$ 上， $A B = 5 ， B C = 2$ ，点 $C$ 为 $B D$ 中点，则 $A D$ 的长为．

查看试题解析

三、解答题

18. 计算： $- 1^{2} + | - 2 | + (\frac{1}{3} - \frac{3}{4}) \times 12$

查看试题解析
19. 解方程： $\frac{2 x + 1}{3} = \frac{x - 1}{4} + 1$

查看试题解析
20. 根据下列要求画图（不写作法，保留作图痕迹）

⑴连接线段 $O B$ ；

⑵画射线 $A O$ ，射线 $A B$ ；

⑶用圆规在射线 $A B$ 上截取 $A C$ ，使得 $A C = O B$ ，画直线 $O C$ ．

查看试题解析
21. 某中学为了解全校学生到校上学的方式，在全校随机抽取了若干名学生进行问卷调查．问卷给出了五种上学方式供学生选择，每人只能选一项，且不能不选．同时把调查得到的结果绘制成如图所示的条形统计图和扇形统计图（均不完整）．请根据图中提供的信息解答下列问题：

(1)、在这次调查中，一共抽取了多少名学生？

(2)、通过计算补全条形统计图；

(3)、在扇形统计图中，“公交车”部分所对应的圆心角是多少度？

(4)、若全校有1600名学生，估计该校乘坐私家车上学的学生约有多少名？

查看试题解析
22. 出租车司机小张某天在季华路（近似地看成一条直线）上行驶，如果规定向东为“正”，向西为“负”，他这天上午的行程可以表示为： $+ 5$ ， $- 3$ ， $+ 3$ ， $- 1$ ， $+ 2$ ， $- 2$ ， $+ 4$ ， $- 5$ ， $+ 6$ ， $- 8$ （单位：千米）．

(1)、小张将最后一名乘客送达目的地后需要返回出发地换班，请问小张该如何行驶才能回到出发地？

(2)、若汽车耗油量为0.6升/千米，发车前油箱有72.2升汽油，若小张将最后一名乘客送达目的地，再返回出发地，问小张今天上午是否需要加油？若要加油至少需要加多少才能返回出发地？若不用加油，请说明理由．

查看试题解析
23. 数学家华罗庚曾说过：“数形结合百般好，隔裂分家万事休”．数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来从而实现优化解题途径的目的．请你利用“数形结合”的思想解决以下的问题：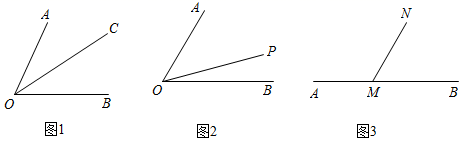

(1)、如图1：射线 $O C$ 是 $∠ A O B$ 的平分线，这时有数量关系： $∠ A O B =$ ．

(2)、如图2： $∠ A O B$ 被射线 $O P$ 分成了两部分，这时有数量关系： $∠ A O B =$ ．

(3)、如图3：直线 $A B$ 上有一点 $M$ ，射线 $M N$ 从射线 $M A$ 开始绕着点 $M$ 顺时针旋转，直到与射线 $M B$ 重合才停止．
①请直接回答 $∠ A M N$ 与 $∠ B M N$ 是如何变化的？

② $∠ A M N$ 与 $∠ B M N$ 之间有什么关系？请说明理由．

查看试题解析
24. 有一个整数 $x$ ，它同时满足以下的条件：
①小于 $π$ ；

②大于 $- 4 \frac{3}{4}$ ；

③在数轴上，与表示 $- 1$ 的点的距离不大于3.

(1)、将满足的整数 $x$ 代入代数式 $- 2 {(x + 1)}^{2} + 7$ ，求出相应的值；

(2)、观察上题的计算结果，你有什么发现？将你的发现写出来．

查看试题解析
25. 已知： $∠ A O B = ∠ C O D = 80 °$

(1)、如图1， $∠ A O C = ∠ B O D$ 吗？请说明理由．

(2)、如图2，直线 $M N$ 平分 $∠ A O D$ ，直线 $M N$ 平分 $∠ B O C$ 吗？请说明理由．

(3)、若 $∠ B O D = 150 °$ ， $∠ B O E = 20 °$ ，求 $∠ C O E$ 的大小．

查看试题解析