湖南省五市十校2020-2021学年高一上学期数学第一次联考试卷
试卷更新日期:2021-09-15 类型:月考试卷
一、单选题
-
1. 设全集 ,集合 , ,则 ( )A、 B、 C、 D、2. 命题“ , ”的否定为( )A、 , B、 , C、 , D、 ,3. “”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 若 , , ,则( )A、 B、 C、 D、5. 某校第34届校田径运动会在今年11月顺利举行,该校高一2001班共有50名学生,有20名学生踊跃报名,其中报名参加田赛的同学有10人,报名参加径赛的同学有13人,则既参加田赛又参加径赛的同学有( )A、2人 B、3人 C、4人 D、5人6. 函数 的图象大致为( )A、
 B、
B、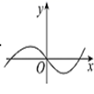 C、
C、 D、
D、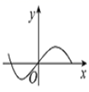 7. 若 ,则( )A、 B、 C、 D、8. 函数 的零点所在的区间为( )A、 B、 C、 D、
7. 若 ,则( )A、 B、 C、 D、8. 函数 的零点所在的区间为( )A、 B、 C、 D、二、多选题
-
9. 已知单元素集合 ,则集合 的所有子集构成的集合 ,下列表示正确的是( )A、 B、 C、 D、10. 下列命题正确的是( )A、奇函数的图象一定过坐标原点 B、若函数 的定义域为 ,则函数 的定义域为 C、函数 ( 且 )的图像过定点 D、函数 与 是同一函数11. 已知对任意 ,且 , 恒成立,则 的取值可以是( )A、 B、 C、 D、12. 已知 是定义在 上的奇函数,且满足 .若 ,记 , ,则下列结论正确的是( )A、 B、 C、 D、
三、填空题
-
13. 已知 ,则 的解析式为.14. 已知幂函数 的定义域为 ,且单调递减,则 .15. 若函数 是偶函数,定义域为 ,则 .16. 已知函数 ,若方程 有4个根分别为 , , , ,且 ,则 的取值范围是.
四、解答题
-
17.(1)、化简: ( , 均为正数);(2)、求值: .18. 已知函数 .(1)、若 ,求 在区间 上的最大值与最小值;(2)、若 在区间 上是单调函数,求实数 的取值范围;(3)、求不等式 的解集.19. 为创建全国卫生文明城市,倡导市民绿色出行,我市根据实际情况,新增开第11路专线,根据市场调查和试营运发现,汽车的发车时间间隔 (单位:分钟)满足 , ,汽车的载客量 与发车时间间隔 满足 .(1)、请你说明 的实际意义﹔(2)、若该线路每分钟的净收益为 (元),当发车时间间隔为多少时,该线路每分钟的净收益最大?并求最大净收益.