湖南省部分重点学校联考2020-2021学年高一上学期数学12月月考试卷

试卷更新日期：2021-09-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知集合 $A = {x \in N | x \geq 4}$ ， $B = {x \in Z | - 1 \leq x \leq 2}$ ，则 $(C_{N} A) \cup B =$ （）

A、 ${0 ， 1 ， 2 ， 3}$ B、 ${- 1 ， 0 ， 1 ， 2}$ C、 ${- 1 ， 0 ， 1 ， 2 ， 3}$ D、 $(- \infty ， 4)$

查看试题解析
2. 命题“∀x＞0，x²＞0”的否定是（）

A、∀x＞0，x²＜0 B、∀x＞0，x²≤0 C、∃x₀＞0，x²＜0 D、∃x₀＞0，x²≤0

查看试题解析
3. 函数 $f (x) = x^{0} - \log_{2} (x + 1)$ 的定义域为（）

A、 $[- 1 ， 0) \cup (0 ， + \infty)$ B、 $(- 1 ， + \infty)$ C、 $[- 1 ， + \infty)$ D、 $(- 1 ， 0) \cup (0 ， + \infty)$

查看试题解析
4. 已知某函数的图象如图所示，则该函数的解析式可能是（）

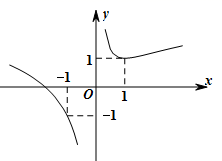A、 $f (x) = \ln | x | - \frac{1}{x}$ B、 $f (x) = \ln | x | + \frac{1}{x}$ C、 $f (x) = \frac{1}{x} - \ln | x |$ D、 $f (x) = \ln | x | + \frac{1}{| x |}$

查看试题解析
5. “ $α$ 是第一或第二象限角”是“ $\sin α > 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
6. 已知函数 $f (x) = m x^{2} - m x$ ，当 $1 \leq x \leq 3$ 时， $f (x) < 6 - m$ 恒成立，则 $m$ 的取值范围为（　　）

A、 $(- \infty ， \frac{6}{7})$ B、 $(- \infty ， \frac{7}{6})$ C、 $(- \infty ， 6)$ D、 $(- \infty ， \frac{1}{6})$

查看试题解析
7. 已知正数 $a$ ， $b$ 满足 $\frac{1}{a} + \frac{1}{b + 2} = \frac{1}{2}$ ，则 $a + b$ 的最小值为（）

A、2 B、4 C、6 D、8

查看试题解析
8. 已知 $\min {a ， b ， c}$ 表示实数 $a$ ， $b$ ， $c$ 中的最小值，设函数 $f (x) = \min {x + 1 ， 3 x - 1 ， g (x)}$ ，若 $f (x)$ 的最大值为4，则 $g (x)$ 的解析式可以为（）

A、 $g (x) = 1 - x$ B、 $g (x) = - x^{2} + 4 x + 1$ C、 $g (x) = 4 x - 8$ D、 $g (x) = 2^{x} - 4$

查看试题解析

二、多选题

9. 下列选项中正确的是（）

A、 $\sin (α - 3 π) = \sin α$ B、 $\cos (α - \frac{7}{2} π) = - \sin α$ C、 $\tan (- α - π) = - \tan α$ D、 $\sin (\frac{5}{2} π - α) = \cos α$

查看试题解析
10. 已知函数 $f (x) = 2 \sin (2 x - \frac{π}{6})$ ，则下列说法正确的是（）

A、 $f (x)$ 的图象关于点 $(\frac{π}{12} ， 0)$ 对称 B、 $f (x)$ 的图象关于直线 $x = \frac{π}{3}$ 对称 C、 $f (x)$ 在 $[- \frac{π}{12} ， \frac{π}{4}]$ 上单调递增 D、 $f (x)$ 在 $[- \frac{π}{6} ， \frac{π}{3}]$ 上单调递减

查看试题解析
11. 设非零实数 $a$ ， $b$ 满足 $\frac{1}{a} > - 1 > \frac{1}{b}$ ，则（）

A、 $a < b$ B、 $\frac{1}{a} + b + 2 > 0$ C、 $a^{2} + \frac{1}{b^{2}} > 1$ D、 $b > - \frac{1}{2}$

查看试题解析
12. 已知函数 $f (x) = 2^{x} + x - 2$ 的零点为 $a$ ，函数 $g (x) = \log_{2} x + x - 2$ 的零点为 $b$ ，则（）

A、 $a + b = 2$ B、 $2^{a} + \log_{2} b = 2$ C、 $a^{2} + b^{2} > 3$ D、 $0 < a b < 1$

查看试题解析

三、填空题

13. 若 $\tan θ = 3$ ，则 $\frac{\sin θ - 2 \cos θ}{3 \sin θ + \cos θ} =$ .

查看试题解析
14. 已知函数 $f (x) = {\begin{array}{l} x^{2} ， x < 2 \\ f (x - 3) ， x \geq 2 \end{array}$ ，则 $f (2020) =$ .

查看试题解析
15. 某商标图案（如图所示）是在一个苹果图案中，以曲线段AB为分界线，裁去一部分图形制作而成的.如果该分界线是一段半径为R的圆弧，且A，B两点间的距离为 $| A B | = \sqrt{3} R$ ，那么分界线的长度为.

查看试题解析
16. 已知幂函数 $f (x) = (m^{2} - 3 m + 3) x^{m + 1}$ 的图象关于原点对称，则满足 ${(a + 1)}^{\frac{m}{3}} > {(3 - 2 a)}^{\frac{m}{3}}$ 的实数 $a$ 的值构成的集合为.

查看试题解析

四、解答题

17. 在① $2 \in M ， 3 \notin M$ ，②函数 $y = \frac{a}{x} - 1$ 的图象经过点 $P (2 ， - \frac{5}{4})$ ，③ $a < 0$ ， $2 a^{2} - 5 a - 3 = 0$ 这三个条件中任选一个，补充在下面的问题中并解答.
问题：已知集合 $M = {x \in N | x \leq 3 + 2 a}$ ， $N = {x | 1 < 2 x + 1 < 6}$ ，且 ▲ ，求 $M \cap N$ .

查看试题解析
18. 化简求值：

(1)、 ${(0.064)}^{- \frac{1}{3}} - {(π - 1)}^{0} - {(3 \frac{3}{8})}^{\frac{1}{3}} + {(\frac{1}{16})}^{- \frac{3}{4}}$ ；

(2)、 $\log_{27} 9 + 2 \lg 5 + \lg 4 - 2^{1 - \log_{2} 3}$ .

查看试题解析
19. 已知函数 $f (x) = \log_{2} (x^{2} - 4)$ .

(1)、求函数 $f (x)$ 的单调区间；

(2)、若 $f (- 2 m + 3) > f (m)$ ，求 $m$ 的取值范围.

查看试题解析
20. 已知函数 $f (x) = A \sin (ω x + φ) (A > 0 ， ω > 0 ， 0 < φ < π)$ 的部分图象如图所示.

(1)、求函数 $f (x)$ 的解析式；

(2)、当 $x \in [- \frac{9}{2} ， \frac{1}{2}]$ 时，求函数 $y = 2 f (x + 2)$ 的最值.

查看试题解析
21. 2020年某开发区一家汽车生产企业计划引进一批新能源汽车制造设备，通过市场分析，全年需投入固定成本500万元，每生产 $x$ 百辆，需另投入成本 $f (x)$ 万元，且 $f (x) = {\begin{array}{l} 10 x^{2} + 200 x ， 0 < x \leq 60 \\ 801 x + \frac{10000}{x} - 9700 ， x > 60 \end{array}$ ，已知每辆车的售价为8万元，且全年内生产的车辆当年能全部销售完.

(1)、求出2020年的利润 $L (x)$ （万元）关于年产量 $x$ （百辆）的函数关系式；（利润＝销售额－成本）

(2)、当2020年产量为多少时，企业所获利润最大？并求出最大利润.

查看试题解析
22. 定义在 $R$ 上的函数 $f (x)$ 对任意的 $a ， b \in R$ ，都有 $f (a + b) = f (a) + f (b) - 1$ ，且当 $x > 0$ 时， $f (x) > 1$ .

(1)、若 $g (x) = f (x) - 1$ ，证明： $g (x)$ 是奇函数.

(2)、若 $f (1) = 2$ ，解不等式 $f (m^{2} - 4 m - 9) < 4$ .

查看试题解析