广东省东莞市七校2020-2021学年高一上学期数学联考试卷

试卷更新日期：2021-09-15 类型：月考试卷

进入出卷网下载

一、单选题

1. 已知A={-1，0，1}，B={x|x²<1}，则A∩B等于（）

A、{-1，0，1} B、 $\emptyset$ C、{0} D、{0，1}

查看试题解析
2. “ $\lg x < 0$ ”是 “ $x < 2$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
3. 命题“ $\exists x \in R$ ， $x^{2} + 2 x + 2 \leq 0$ ”的否定是（）

A、 $\exists x \notin R$ ， $x^{2} + 2 x + 2 \leq 0$ B、 $\exists x \in R$ ， $x^{2} + 2 x + 2 > 0$ C、 $\forall x \in R$ ， $x^{2} + 2 x + 2 \leq 0$ D、 $\forall x \in R$ ， $x^{2} + 2 x + 2 > 0$

查看试题解析
4. 设 $a ， b \in R$ ，则下列命题正确的是（）

A、若 $x > y$ ， $a > b$ ，则 $a - x > b - y$ B、若 $a > b$ ，则 $\frac{1}{a} < \frac{1}{b}$ C、若 $x > y$ ， $a > b$ 则 $a x > b y$ D、若 $a > | b |$ ，则 $a^{2} > b^{2}$

查看试题解析
5. 函数 $f (x) = \log_{2} x - \frac{1}{x}$ 的零点所在的区间为（）

A、 $(0 ， 1)$ B、 $(1 ， 2)$ C、 $(2 ， 3)$ D、 $(3 ， 4)$

查看试题解析
6. 函数 $f (x) = \frac{e^{x} - e^{- x}}{x^{2}}$ 的图象大致为（）

A、 B、 C、 D、

查看试题解析
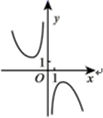7. 已知 $a = {(\frac{1}{2})}^{\frac{1}{2}}$ ， $b = {(\frac{1}{2})}^{\frac{1}{3}}$ ， $c = \log_{2} 3$ ，则a ， b ， c的大小关系为（）

A、 $a < b < c$ B、 $c < b < a$ C、 $a < c < b$ D、 $b < c < a$

查看试题解析
8. 中国的5G技术领先世界，5G技术的数学原理之一便是著名的香农公式： $C = W \log_{2} (1 + \frac{S}{N})$ .它表示：在受噪声干扰的信道中，最大信息传递速度C取决于信道带宽W ，信道内信号的平均功率S ，信道内部的高斯噪声功率N的大小，其中 $\frac{S}{N}$ 叫做信噪比.当信噪比较大时，公式中真数中的1可以忽略不计.按照香农公式，若不改变带宽W ，而将信噪比 $\frac{S}{N}$ 从1000提升至8000，则C大约增加了( $\lg 2 \approx 0.3010$ )（）

A、10% B、30% C、60% D、90%

查看试题解析

二、多选题

9. 已知集合A={x|x≥0}，集合B={x|x>1}，则以下命题正确的是（）

A、 $\exists x \in A$ ， $x \notin B$ B、 $\exists x \in B$ ， $x \notin A$ C、 $\forall x \in A$ ， $x \in B$ D、 $\forall x \in B$ ， $x \in A$

查看试题解析
10. 下列函数和 $y = x$ 是同一函数的是（）

A、 $y = \sqrt{x^{2}}$ B、 $y = \lg 10^{x}$ C、 $y = \sqrt[3]{x^{3}}$ D、 $y = \frac{x^{2}}{x}$

查看试题解析
11. 下列函数中，即是奇函数，又是R上的增函数的是（）

A、 $y = 3^{x}$ B、 $y = x | x |$ C、 $y = x^{3}$ D、 $y = x^{2}$

查看试题解析
12. 已知函数 $f (x) = {\begin{matrix} - x^{2} - 2 x ， x \leq m \\ x - 4 ， x > m \end{matrix}$ ，如果函数 $f (x)$ 恰有两个零点，那么实数 $m$ 的取值范围可以是（）

A、 $m < - 2$ B、 $- 2 \leq m < 0$ C、 $0 \leq m < 4$ D、 $m \geq 4$ .

查看试题解析

三、填空题

13. 函数 $f (x) = \log_{2} (x - 1) + \sqrt{4 - x}$ 的定义域为.（结果用集合或区间表示）

查看试题解析
14. 不等式x²＋3x－4＜0的解集为.

查看试题解析
15. 已知函数 $f (x) = \log_{a} \frac{x - 1}{x + 1} + 1$ 且 $f (5) = 7 ，$ 则 $f (- 5)$ =.

查看试题解析
16. 设函数 $f (x) = {\begin{array}{l} - x^{2} + 2 a x - 7 ， x \leq 3 \\ a^{x - 1} ， x > 3 \end{array}$ 是定义在R上的增函数，则实数 $a$ 的的取值范围是.

查看试题解析

四、解答题

17. 设 $m$ 为实数，集合 $A = {x | - 1 \leq x \leq 4}$ ， $B = {x | m \leq x \leq m + 2}$ .

(1)、若 $m = 3$ ，求 $A \cup B$ ， $C_{R} (A \cap B)$ ；

(2)、若 $A \cap B = \emptyset$ ，求实数 $m$ 的取值范围.

查看试题解析
18. 计算下列各式的值：

(1)、 ${(2 \frac{1}{4})}^{\frac{1}{2}} - {(- 9.6)}^{0} - {(\frac{8}{27})}^{\frac{2}{3}} + {(\frac{3}{2})}^{- 2}$ ；

(2)、 $\log_{3} \sqrt[4]{27} + \lg 25 + \lg 4 + 7^{\log_{7} \frac{1}{4}}$ .

查看试题解析
19. 在城市旧城改造中，某小区为了升级居住环境，拟在小区的闲置地中规划一个面积为 $200 m^{2}$ 的矩形区域（如图所示），按规划要求：在矩形内的四周安排 $2 m$ 宽的绿化，绿化造价为200元/ $m^{2}$ ，中间区域地面硬化以方便后期放置各类健身器材，硬化造价为100元/ $m^{2}$ ．设矩形的长为 $x (m)$ ．

(1)、将总造价 $y$ （元）表示为长度 $x (m)$ 的函数，并求出定义域；

(2)、当 $x (m)$ 取何值时，总造价最低，并求出最低总造价．

查看试题解析
20. 已知函数 $t = \log_{2} x ， f (x) = {(\log_{2} x)}^{2} - 6 \log_{2} x + 8$ ．

(1)、求函数 $t = \log_{2} x$ 在区间［1，32］上的最大值与最小值；

(2)、求函数f（x）的零点；

(3)、求函数f（x）在区间［1，32］上的值域．

查看试题解析
21. 已知函数 $f (x) = a - \frac{2}{2^{x} + 1}$ （ $a \in R$ ）为奇函数.

(1)、求 $a$ 的值；

(2)、判断函数 $f (x)$ 的单调性，并用定义证明；

(3)、若对任意 $x \in [t ， + \infty)$ ，不等式 $f (x) \geq \frac{3}{5}$ 恒成立，求实数 $t$ 的最小值.

查看试题解析
22. 已知函数 $f (x) = {\begin{array}{l} - x^{2} + x ， x \geq 0 \\ x^{2} - x ， x < 0 \end{array}$ .

(1)、画出函数 $f (x)$ 的图象，写出 $f (x)$ 的单调区间，并指出每个区间的单调性；

(2)、若关于 $x$ 的不等式 ${[f (x)]}^{2} - (a + 2) f (x) + 2 a \leq 0$ 恰有3个整数解，求实数 $a$ 的取值范围.

查看试题解析