江苏省苏州市工业园区星海2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，关于 $x$ 的一元二次方程是（）

A、 $x + 2 = 3$ B、 $x + y = 1$ C、 $x^{2} - 2 x - 3 = 0$ D、 $x^{2} + \frac{1}{x} = 1$

查看试题解析
2. 二次函数 $y = x^{2} - 2 x$ 的顶点坐标是（）

A、 $(1, 1)$ B、 $(1, - 1)$ C、 $(- 1, - 1)$ D、 $(- 1, 1)$

查看试题解析
3. 已知点 $A (- 3 ， y_{1})$ ， $B (2 ， y_{2})$ 均在抛物线 $y = - 2 {(x - 1)}^{2} + 3$ 上，则下列结论正确的是（）

A、 $y_{1} < y_{2} < 3$ B、 $y_{2} < y_{1} < 3$ C、 $3 < y_{2} < y_{1}$ D、 $3 < y_{2} < y_{1}$

查看试题解析
4. 将抛物线 $y = 2 {(x + 1)}^{2} - 3$ 先向上平移3个单位长度，再向右平移1个单位长度可得抛物线（）

A、 $y = 2 x^{2}$ B、 $y = 2 {(x + 2)}^{2}$ C、 $y = 2 x^{2} - 6$ D、 $y = 2 {(x + 2)}^{2} - 6$

查看试题解析
5. 已知 $2 - \sqrt{3}$ 是一元二次方程 $x^{2} - 4 x + c = 0$ 的一个根，则方程的另一个根为（）

A、 $\sqrt{3}$ B、 $\sqrt{3} - 2$ C、 $2 - \sqrt{3}$ D、 $2 + \sqrt{3}$

查看试题解析
6. 若关于x的一元二次方程kx²+2x–1=0有实数根，则实数k的取值范围是

A、k≥–1 B、k>–1 C、k≥–1且k≠0 D、k>–1且k≠0

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 7$ ， $A C = 4$ ，以点 $C$ 为圆心、 $C A$ 为半径的圆交 $A B$ 于点 $D$ ，求弦 $A D$ 的长为（）

A、 $\frac{4 \sqrt{33}}{7}$ B、 $\frac{32}{7}$ C、 $\frac{2 \sqrt{33}}{7}$ D、 $\frac{16}{7}$

查看试题解析
8. 已知二次函数 $y = a x^{2} + b x + c$ 的自变量 $x$ 与函数 $y$ 的部分对应值列表如下：

$x$

…

$- 1$

0

1

2

3

…

$y$

…

3

0

$- 1$

$m$

3

…

则关于 $x$ 的方程 $a x^{2} + b x + c = 0$ 的解是（）

A、 $x_{1} = 0$ ， $x_{2} = 2$ B、 $x_{1} = x_{2} = 2$ C、 $x_{1} = x_{2} = 0$ D、不能确定

查看试题解析
9. 给出下列说法：①圆是轴对称图形，对称轴是圆的每一条直径；②三角形的外心到三角形各顶点的距离相等；③经过三个点一定可以画一个圆；④平分弦的直径垂直于弦；⑤垂直于弦的直径平分弦，并且平分弦所对的两条弧.正确的有（）

A、4 B、3 C、2 D、1

查看试题解析
10. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图像如图所示，抛物线的对称轴是直线 $x = 1$ ，与 $x$ 轴的一个交点坐标为（4，0）.下列结论中：① $c > a$ ；② $2 a - b = 0$ ；③方程 $a x^{2} + b x + c = 1 (a \neq 0)$ 有两个不相等的实数根；④抛物线与 $x$ 轴的另一个交点坐标为（–1，0）；⑤若点 $A (m ， n)$ 在该抛物线上，则 $a m^{2} + b m \leq a + b$ .其中正确的有（）

A、①③④ B、②③④ C、①③⑤ D、①④⑤

查看试题解析

二、填空题

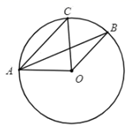
11. 已知关于 $x$ 的方程 $(m + 1) x^{2} + 4 m x + 1 = 0$ 是一元二次方程，则 $m$ 的取值范围是.

查看试题解析
12. 三角形的两边长分别是4和5，第三边长是方程 $x^{2} - 14 x + 45 = 0$ 的根，则该三角形的周长为.

查看试题解析
13. 如图，点 $A$ 、 $B$ 、 $C$ 在 $⊙ O$ 上， $A C // O B$ ， $∠ B A O = 20 °$ ，则 $∠ B O C$ 的度数为.

查看试题解析
14. 某商店9月份的利润是2500元，要使11月份的利润达到3600元，平均每月利润增长的百分率为.

查看试题解析
15. 如图所示为抛物线 $y = a x^{2} - 2 a x + 3$ ，则一元二次方程 $a x^{2} - 2 a x + 3 = 0$ 两根为.

查看试题解析
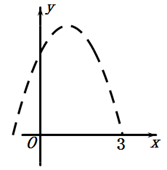16. 若点 $(- 1 ， - 2)$ 在二次函数 $y = a x^{2} + 2 b x + 1$ （ $a \neq 0$ ）的图像上，则代数式 $2 a - 4 b + 1$ 的值为.

查看试题解析
17. 研究二次函数 $y = x^{2} - a x + 2 a + 1$ 的图像时发现：无论 $a$ 如何变化，该图像总经过一个定点.这个定点坐标为.

查看试题解析
18. 如图，在平面直角坐标系xOy中，半径为4的⊙O与x轴的正半轴交于点A，点B是⊙O上一动点，点C为弦AB的中点，直线 $y = \frac{3}{4} x - 6$ 与x轴、y轴分别交于点D、E，则 $△ C D E$ 面积的最小值为.

查看试题解析

三、解答题

19. 解方程（2x+1）²=3（2x+1）

查看试题解析
20. 解分式方程： $\frac{x}{x - 1} - \frac{2}{x + 1} = \frac{4}{x^{2} - 1}$ .

查看试题解析
21. 先化简，再求值： $(\frac{1}{x + 1} + \frac{1}{x - 1}) \div \frac{x^{2} - x}{x^{2} - 2 x + 1}$ ，其中 $x$ 满足 $x^{2} - 2 x = 0$ .

查看试题解析
22. 如图，在直角坐标系中， $A$ （0，4）、 $B$ （4，4）、 $C$ （6，2），

(1)、写出经过 $A$ 、 $B$ 、 $C$ 三点的圆弧所在圆的圆心 $M$ 的坐标：；

(2)、判断点 $D (5 ， - 2)$ 与圆 $M$ 的位置关系.

查看试题解析
23. 已知关于 $x$ 的一元二次方程 $x^{2} - (a + 3) x + 2 a = 0$ ，

(1)、求证：方程总有两个不相等的实数根；

(2)、设该方程的两个根分别为 $x_{1}$ 、 $x_{2}$ ，若 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = a$ ，求 $a$ 的值.

查看试题解析
24. 二次函数 $y_{1} = x^{2} - (m + 3) x + 3 m$ 的图像与一次函数 $y_{2} = k x + 3$ （ $k \neq 0$ ）的图像的一个交点为 $A$ ，点 $A$ 的横坐标为2，另一个交点 $C$ 在 $y$ 轴上.

(1)、求一次函数和二次函数的表达式；

(2)、直接写出当 $x$ 取何值时，一次函数值大于二次函数值；

(3)、设二次函数的图象与 $x$ 轴的一个交点为 $B$ （ $B$ 在直线 $A C$ 右侧），求 $△ A B C$ 的面积.

查看试题解析
25. 某超市经销一种商品，每千克成本为40元，经试销发现，该种商品的每天销售量 $y$ （千克）与销售单价 $x$ （元/千克）满足一次函数关系，其每天销售单价，销售量的四组对应值如下表所示：

销售单价 $x$ （元/千克）

45

50

55

60

销售量 $y$ （千克）

70

60

50

40

(1)、求 $y$ （千克）与 $x$ （元/千克）之间的函数表达式；

(2)、为了尽可能提高销量且保证某天获得600元的销售利润，则该天的销售单价应定为多少？

(3)、当销售单价定为多少时，才能使当天的销售利润最大？最大利润是多少？

查看试题解析
26. 如图，点 $P$ 在 $x$ 轴上，以点 $P$ 为圆心的圆，交 $x$ 轴于 $D$ 、 $C$ 两点，交 $y$ 轴于 $A$ 、 $B$ 两点， $A B = 2 \sqrt{3}$ ， $O C = 3$ .

(1)、求圆心 $P$ 的坐标；

(2)、将 $△ A D C$ 绕点 $P$ 旋转 $180 °$ ，得到 $△ E C D$ .请在图中画出线段 $E D$ 、 $E C$ ，判断四边形 $A C E D$ 的形状，请说明理由，并直接写出点 $E$ 坐标.

(3)、设点 $F$ 为 $\overset{⌢}{D B E}$ 上一个动点，连接线段 $C F$ 与 $D E$ 相交于点 $G$ ，点 $M$ 为 $C G$ 的中点，过点 $G$ 作 $G H ⊥ D C$ 于 $H$ ，连接 $H M$ 、 $E M$ .在点 $F$ 的运动过程中 $∠ H M E$ 的大小是否变化？若不变，求出 $∠ H M E$ 的度数；若变化，请说明理由.

查看试题解析
27. 如图①， $Rt △ A B C$ 中， $∠ C = 90 °$ ， $A C = 6 cm$ .动点 $P$ 以 $a cm/s$ 的速度由 $B$ 出发沿线段 $B A$ 向 $A$ 运动，动点 $Q$ 以 $1 cm/s$ 的速度由 $A$ 出发沿射线 $A C$ 运动.当点 $Q$ 运动 $2 s$ 时，点 $P$ 开始运动； $P$ 点到达终点时， $P$ 、 $Q$ 一起停止.设点 $P$ 运动的时间为 $t s$ ， $△ A P Q$ 的面积为 $y {cm}^{2}$ ， $y$ 与 $t$ 的函数关系图像如图②所示.

(1)、点 $P$ 运动的速度 $a =$ $cm/s$ ， $A B =$ $cm$ ；

(2)、当 $t$ 为何值时， $△ A P Q$ 的面积为 $12 {cm}^{2}$ ；

(3)、是否存在 $t$ ，使得直线 $P Q$ 将 $Rt △ A B C$ 的周长与面积同时平分？若存在，求出 $t$ 的值；若不存在，请说明理由.

查看试题解析
28. 如图①，抛物线 $y = a x^{2} + b x + 3$ 与 $x$ 轴交于 $A (3 ， 0)$ 、 $B (- 1 ， 0)$ 两点，与 $y$ 轴交于点 $C$ .

(1)、求抛物线 $y = a x^{2} + b x + 3$ 的解析式；

(2)、如图②，连接 $A C$ ，点 $E$ 是第一象限内抛物线上的动点，过点 $E$ 作 $E F ⊥ A C$ 于点 $F$ ， $E G // y$ 轴交 $A C$ 于点 $G$ ，求 $△ E F G$ 面积的最大值及此时点 $E$ 的坐标；

(3)、如图③，若抛物线的顶点坐标为点 $D$ ，点 $P$ 是抛物线对称轴上的动点，在坐标平面内是否存在点Q，使得以 $A$ 、 $D$ 、 $P$ 、 $Q$ 为顶点的四边形是菱形？若存在，求出点 $P$ 的坐标；若不存在，请说明理由.

查看试题解析

销售单价 $x$ （元/千克）	45	50	55	60
销售量 $y$ （千克）	70	60	50	40

$x$	…	$- 1$	0	1	2	3	…
$y$	…	3	0	$- 1$	$m$	3	…