江苏省苏州市常熟市2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-14 类型:期中考试
一、单选题
-
1. 已知关于 的方程 是一元二次方程,则 的取值范围是( )A、 B、 C、 D、2. 方程 经过变形后,其结果正确的是( )A、 B、 C、 D、3. 小明连续5天的体温数据如下(单位:℃):36.7,36.3,36.6,36.2,36.3,这组数据的极差是( )A、 B、 C、 D、4. 如图,在 中, , , ,点E是 中点.以B为圆心, 为半径画圆,则点E与 的位置关系是( )
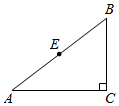 A、点E在 内 B、点E在 上 C、点E在 外 D、无法判断5. 某超市销售同种品牌三种不同规格的盒装牛奶,它们的单价分别为10元、6元、5元,当天销售情况如图所示,则当天销售该品牌盒装牛奶的平均价格为( )
A、点E在 内 B、点E在 上 C、点E在 外 D、无法判断5. 某超市销售同种品牌三种不同规格的盒装牛奶,它们的单价分别为10元、6元、5元,当天销售情况如图所示,则当天销售该品牌盒装牛奶的平均价格为( )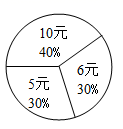 A、6.3元 B、7元 C、7.3元 D、8元6. 如图,四边形ABCD内接于⊙O,连接OA,OC,若∠AOC:∠ADC=2:3,则∠ABC的度数为( )
A、6.3元 B、7元 C、7.3元 D、8元6. 如图,四边形ABCD内接于⊙O,连接OA,OC,若∠AOC:∠ADC=2:3,则∠ABC的度数为( )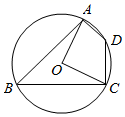 A、30° B、40° C、45° D、50°7. 两个连续奇数的积为323,设其中较小的一个奇数为x,可得方程( )A、 B、 C、 D、8. 如图,在平面直角坐标系中, 三个顶点的坐标分别是点 、点 、点 .则 的外心的坐标是( )
A、30° B、40° C、45° D、50°7. 两个连续奇数的积为323,设其中较小的一个奇数为x,可得方程( )A、 B、 C、 D、8. 如图,在平面直角坐标系中, 三个顶点的坐标分别是点 、点 、点 .则 的外心的坐标是( )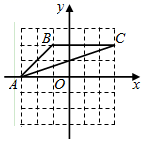 A、 B、 C、 D、9. 如图,在扇形 中, , ,若弦 ,则 的长为( )
A、 B、 C、 D、9. 如图,在扇形 中, , ,若弦 ,则 的长为( )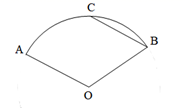 A、 B、 C、 D、10. 如图是一个装置的示意图,其中圆形吊舱初始位置与水平横杆 、卡槽 相切.水平横杆 米, 米,吊舱半径为10米.放开挡板 后,吊舱沿着水平横杆 向点A方向匀速平移,平移速度是每秒1米.从放开挡板,直至吊舱触碰竖直放置的 为止( ),吊舱平移的时间为( )
A、 B、 C、 D、10. 如图是一个装置的示意图,其中圆形吊舱初始位置与水平横杆 、卡槽 相切.水平横杆 米, 米,吊舱半径为10米.放开挡板 后,吊舱沿着水平横杆 向点A方向匀速平移,平移速度是每秒1米.从放开挡板,直至吊舱触碰竖直放置的 为止( ),吊舱平移的时间为( )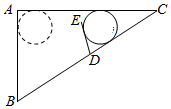 A、30秒 B、40秒 C、50秒 D、60秒
A、30秒 B、40秒 C、50秒 D、60秒二、填空题
-
11. 某中学为了选拔一名运动员参加市运会 米短比赛,有甲、乙两名运动员备选,他们最近测试的 次百米跑平均时间都是 秒,他们的方差分别是 (秒 ) (秒 ),如果要选择一名成绩优秀且稳定的人去参赛,应派去.12. 已知 的半径是4,圆心O到直线l的距离为2.5,则直线l与 的位置关系是13. 如图,地上画了两个半径分别为 和 的同心圆.假设用小石子投中圆形区域上的每一点是等可能的(若投中圆的边界或没有投中圆形区域,则重投1次),任意投掷小石子一次,则投中白色小圆的概率为.
 14. 若关于x的一元二次方程 的一个根为3,则 .15. 某商店今年7月份的销售额是5万元,9月份的销售额是7.2万元,从7月份到9月份该店销售额平均每月的增长率是.16. 一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是.
14. 若关于x的一元二次方程 的一个根为3,则 .15. 某商店今年7月份的销售额是5万元,9月份的销售额是7.2万元,从7月份到9月份该店销售额平均每月的增长率是.16. 一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是. 17. 如图,点O是矩形 的对角线 上的一点, 经过点D,且与 边相切于点E,若 , ,则该圆半径是.
17. 如图,点O是矩形 的对角线 上的一点, 经过点D,且与 边相切于点E,若 , ,则该圆半径是.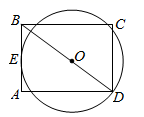 18. 如图,已知 的半径为5, 是直径,点A是圆上任意一点,点D、E是直径 上的动点,且 ,则 的最小值为.
18. 如图,已知 的半径为5, 是直径,点A是圆上任意一点,点D、E是直径 上的动点,且 ,则 的最小值为.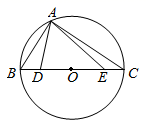
三、解答题
-
19. 解下列方程:(1)、 ;(2)、 .20. 已知关于x的方程 的一个根是2,求另一个根和m的值.21. 体育课上,九年级(1)班和(3)班决定进行“1分钟跳绳”比赛,两个班各派出6名同学,成绩分别为(单位:次):
九(1):187,178,175,179,187,191;
九(3):181,180,180,181,186,184
(1)、九年级(1)班参赛选手成绩的众数为次,中位数为次;(2)、求九年级(3)班参赛选手成绩的方差.22. 小红和父母计划寒假期间从A:拙政园、B:狮子林、C:上方山森林动物世界、D:天平山风景名胜区这4个景点中随机选择景点游玩.(1)、若小红一家从中随机选择一个景点游玩,则选中C:上方山森林动物世界的概率;(2)、若小红一家从中随机选择两个景点游玩,请用列举法(画树状图或列表)求选中A、C两个景点的概率.23. 关于x的一元二次方程x2﹣(2k+1)x+2k=0.(1)、求证:无论k取任何实数,方程总有两个实数根;(2)、若该方程的两个根x1 , x2满足3x1+3x2﹣x1x2=6,求k的值.24. 如图,AB是⊙O的直径,点C,D在⊙O上,且 ,连接CD,交AB于点E,连接BC,BD.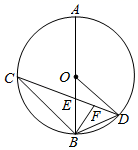 (1)、若∠AOD=130°,求∠BEC的度数;(2)、∠ABD的平分线交CD于点F,求证:BC=CF.25. 某医疗器械生产厂生产某种医疗器械,80条生产线齐开,每条生产线每个月可生产8台该种医疗器械.该厂经过调研发现:当生产线适当减少后(减少的条数在总条数的20%以内时),每减少10条生产线,每条生产线每个月反而会多生产4台.若该厂需要每个月的产能达到840台,那么应减少几条生产线?26. 如图,四边形 内接于 , 是直径, 平分 , 分别交 , 于点E,F,已知 的半径是2
(1)、若∠AOD=130°,求∠BEC的度数;(2)、∠ABD的平分线交CD于点F,求证:BC=CF.25. 某医疗器械生产厂生产某种医疗器械,80条生产线齐开,每条生产线每个月可生产8台该种医疗器械.该厂经过调研发现:当生产线适当减少后(减少的条数在总条数的20%以内时),每减少10条生产线,每条生产线每个月反而会多生产4台.若该厂需要每个月的产能达到840台,那么应减少几条生产线?26. 如图,四边形 内接于 , 是直径, 平分 , 分别交 , 于点E,F,已知 的半径是2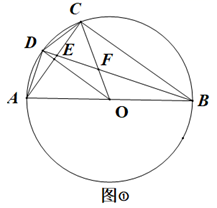
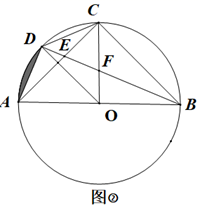 (1)、求证: ;(2)、如图②,若 .
(1)、求证: ;(2)、如图②,若 .①求 的值;
②求阴影部分面积.
27. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O与CD边相切于点E,BC交⊙O于点F(AF>BF),连接AE,EF.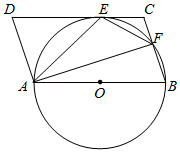 (1)、求证:∠AFE=45°;(2)、求证:EF2=AF•CF;(3)、若⊙O的半径是 ,且 ,求AD的长.28. 如图,在平面直角坐标系中,点 ,点 ,已知 中, , , ,且 在x轴上,现将点C与原点O重合,然后将 以每秒4个单位长度的速度沿x轴正方向移动;同时,点P从点A出发,以每秒5个单位长度的速度沿 方向移动,设移动时间为t秒,以P为圆心, 为半径作圆,交 于点F,G.当点C到达点A时, 和 同时停止移动.
(1)、求证:∠AFE=45°;(2)、求证:EF2=AF•CF;(3)、若⊙O的半径是 ,且 ,求AD的长.28. 如图,在平面直角坐标系中,点 ,点 ,已知 中, , , ,且 在x轴上,现将点C与原点O重合,然后将 以每秒4个单位长度的速度沿x轴正方向移动;同时,点P从点A出发,以每秒5个单位长度的速度沿 方向移动,设移动时间为t秒,以P为圆心, 为半径作圆,交 于点F,G.当点C到达点A时, 和 同时停止移动.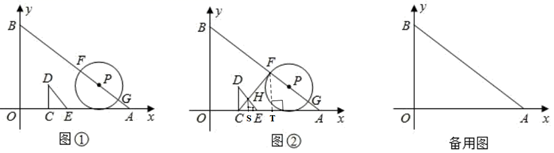 (1)、 , ;(用含t的代数式表示)(2)、如图②,连接 ,交 于点H.若 ,求t的值;(3)、在移动过程中,是否存在某一时刻, 与 所在直线及x轴同时相切?若存在,求出t的值;若不存在,说明理由.
(1)、 , ;(用含t的代数式表示)(2)、如图②,连接 ,交 于点H.若 ,求t的值;(3)、在移动过程中,是否存在某一时刻, 与 所在直线及x轴同时相切?若存在,求出t的值;若不存在,说明理由.