江苏省南京市高淳区2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-14 类型:期中考试
一、单选题
-
1. 已知⊙O的直径为4,点O到直线m的距离为2,则直线m与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、无法判断2. 下列方程中,有两个相等实数根的是( )A、 B、 C、 D、3. 关于函数 ,下列说法:①函数的最小值为1;②函数图象的对称轴为直线x=3;③当x≥0时,y随x的增大而增大;④当x≤0时,y随x的增大而减小,其中正确的有( )个.A、1 B、2 C、3 D、44. 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BAC=20°,则∠D的度数为( )
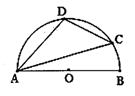 A、100° B、110° C、120° D、130°5. 已知二次函数 的图象与x轴有两个交点,若其中一个交点的横坐标为1,则另一个交点的横坐标为( )A、﹣1 B、﹣6 C、5 D、46. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、100° B、110° C、120° D、130°5. 已知二次函数 的图象与x轴有两个交点,若其中一个交点的横坐标为1,则另一个交点的横坐标为( )A、﹣1 B、﹣6 C、5 D、46. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( ) A、
A、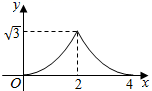 B、
B、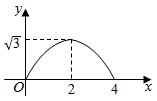 C、
C、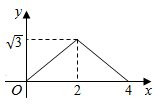 D、
D、
二、填空题
-
7. 用配方法解方程x2+4x+1=0,则方程可变形为(x+2)2=.8. 已知一元二次方程2x2+3x﹣1=0的两个根是x1 , x2 , 则x1•x2=.9. 超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是分.测试项目 创新能力 综合知识 语言表达 测试成绩(分数) 70 80 92 10. 同时抛掷两枚质地均匀的硬币,则两枚硬币全部正面向上的概率是 .11. 一个圆锥的底面半径为3cm,侧面展开图是半圆,则圆锥的侧面积是cm2 .12. 如图,平面直角坐标系中,桥孔抛物线对应的二次函数关系式是y=﹣ x2 , 桥下的水面宽AB为6m,当水位上涨2m时,水面宽CD为m(结果保留根号). 13. 如图,在正八边形ABCDEFGH中,AC,GC是两条对角线,则∠ACG=.
13. 如图,在正八边形ABCDEFGH中,AC,GC是两条对角线,则∠ACG=.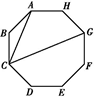 14. 如图,在 中,半径 垂直 于 ,则 的半径是.
14. 如图,在 中,半径 垂直 于 ,则 的半径是. 15. 某商贸公司2017年盈利100万元,2019年盈利144万元,且2017年到2019年每年盈利的增长率相同,则该公司2018年盈利万元.16. 如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为.
15. 某商贸公司2017年盈利100万元,2019年盈利144万元,且2017年到2019年每年盈利的增长率相同,则该公司2018年盈利万元.16. 如图,已知正方形ABCD的边长为2,E是BC边上的动点,BF⊥AE交CD于点F,垂足为G,连结CG.则CG的最小值为.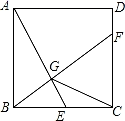
三、解答题
-
17. 解方程 (2x-1)2=3-6x.18. 已知二次函数y=ax2+bx+c中自变量x和函数值y的部分对应值如表:
x … -1 0 1 2 3 … y … 10 5 2 1 2 … (1)、求该二次函数的函数关系式;(2)、在所给的直角坐标系中画出此函数的图象;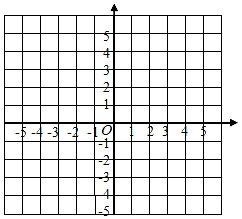 (3)、作该二次函数y=ax2+bx+c的图象关于x轴对称的新图象,则新图象的函数关系式为.19. 甲、乙两位同学5次数学选拔赛的成绩统计如表,他们5次考试的总成绩相同,请同学们完成下列问题:
(3)、作该二次函数y=ax2+bx+c的图象关于x轴对称的新图象,则新图象的函数关系式为.19. 甲、乙两位同学5次数学选拔赛的成绩统计如表,他们5次考试的总成绩相同,请同学们完成下列问题:第1次
第2次
第3次
第4次
第5次
甲成绩
80
40
70
50
60
乙成绩
70
50
70
a
70
(1)、统计表中,a= , 甲同学成绩的极差为;(2)、小颖计算了甲同学的成绩平均数为60,方差是S甲2= [(80﹣60)2+(40﹣60)2+(70﹣60)2+(50﹣60)2+(60﹣60)2]=200.请你求出乙同学成绩的平均数和方差;(3)、从平均数和方差的角度分析,甲、乙两位同学谁的成绩更稳定.20. 如图,AB、CD都是⊙O的弦,且AB∥CD,求证: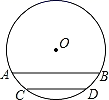 21. 甲、乙两名同学参加 1000 米比赛,由于参赛选手较多,将选手随机分 A、B、C 三组进行比赛.(1)、求甲同学恰好在A 组的概率.(2)、求甲、乙两人至少有一人在 B 组的概率(用画树状图或列表法).22. 如图,用长为24m.的篱笆,一面利用墙(墙的最大可用长度为10m)围成中间有一道篱笆的长方形花圃,现要围成面积为45 的花圃,求 的长是多少?
21. 甲、乙两名同学参加 1000 米比赛,由于参赛选手较多,将选手随机分 A、B、C 三组进行比赛.(1)、求甲同学恰好在A 组的概率.(2)、求甲、乙两人至少有一人在 B 组的概率(用画树状图或列表法).22. 如图,用长为24m.的篱笆,一面利用墙(墙的最大可用长度为10m)围成中间有一道篱笆的长方形花圃,现要围成面积为45 的花圃,求 的长是多少?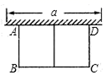 23. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息.
23. 某年级共有300名学生.为了解该年级学生A,B两门课程的学习情况,从中随机抽取60名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理、描述和分析.下面给出了部分信息..A课程成绩的频数分布直方图如下(数据分成6组: , , , , , );
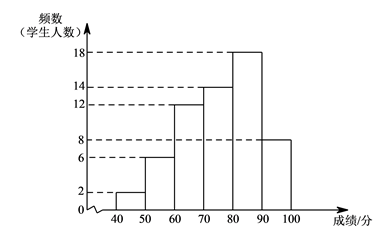
.A课程成绩在 这一组是:
70 71 71 71 76 76 77 78 79 79 79
.A,B两门课程成绩的平均数、中位数、众数如下:
课程
平均数
中位数
众数
A
B
70
83
根据以上信息,回答下列问题:
(1)、写出表中 的值;(2)、在此次测试中,某学生的A课程成绩为76分,B课程成绩为71分,这名学生成绩排名更靠前的课程是(填“A”或“B”),理由是;(3)、假设该年级学生都参加此次测试,估计A课程成绩超过 分的人数.24. 已知二次函数y=(x﹣1)(x﹣m)(m为常数)(1)、求证:不论m为何值,该函数的图象与x轴总有公共点;(2)、当m的值变化时,该函数图象的顶点在下列哪个函数的图象上? _______.A、y=x﹣1 B、y=﹣x﹣1 C、y=﹣(x+1)2 D、y=﹣(x﹣1)225. 如图,△EBF中,∠B=90°,O是BE上一点,以O为圆心,OB为半径的圆与OF交于点C,与EB交于点A,与EF交于点D,连接AD、DC,四边形AOCD为平行四边形.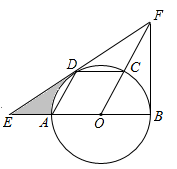 (1)、求证:EF为⊙O的切线;(2)、已知⊙O的半径为1,求图中阴影部分的面积.26. 平面直角坐标系中,已知点A(1,2),B(2,3),C(2,1),抛物线y=ax2+bx+1恰好经过A,B,C中的两点.(1)、求a,b的值;(2)、平移抛物线y=ax2+bx+1,使其顶点在直线y=x+1上,设平移后抛物线顶点的横坐标为m.
(1)、求证:EF为⊙O的切线;(2)、已知⊙O的半径为1,求图中阴影部分的面积.26. 平面直角坐标系中,已知点A(1,2),B(2,3),C(2,1),抛物线y=ax2+bx+1恰好经过A,B,C中的两点.(1)、求a,b的值;(2)、平移抛物线y=ax2+bx+1,使其顶点在直线y=x+1上,设平移后抛物线顶点的横坐标为m.①求平移后抛物线的函数关系式;
②求平移后的抛物线与y轴交点纵坐标的最大值.
27. 如图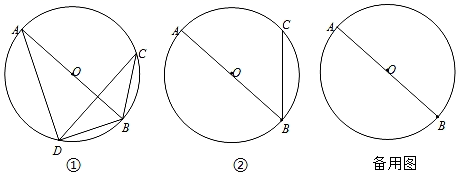 (1)、如图①,AB是⊙O的直径,C、D在⊙O上,且BC=BD,AD=CD.求证:∠ADC=2∠BDC.(2)、如图②,AB是⊙O的直径,点C在⊙O上.若平面内的点D满足AD=CD,且∠ADC=2∠BDC.
(1)、如图①,AB是⊙O的直径,C、D在⊙O上,且BC=BD,AD=CD.求证:∠ADC=2∠BDC.(2)、如图②,AB是⊙O的直径,点C在⊙O上.若平面内的点D满足AD=CD,且∠ADC=2∠BDC.①利用直尺和圆规在图②中作出所有满足条件的点D(保留作图痕迹,不写作法);
②若AB=4,BC长度为m(0<m<4),则平面内满足条件的点D的个数随着m的值变化而变化,请直接写出满足条件点D的个数及对应m的取值范围.