江苏省南京市2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是关于 $x$ 的一元二次方程的是（）

A、 $2 x + y = 2$ B、 $x + y^{2} = 0$ C、 $a x^{3} + b x + c = 0$ D、 $2 x - x^{2} = 1$

查看试题解析
2. 若圆弧的半径为3，所对的圆心角为60°，则弧长为（）

A、 $\frac{1}{2} π$ B、 $π$ C、 $\frac{3}{2} π$ D、 $3 π$

查看试题解析
3. 反映一组数据变化范围的是（）

A、极差 B、方差 C、众数 D、平均数

查看试题解析
4. 下列方程中，两个实数根的和为0的是（）

A、 $x^{2} - x = 0$ B、 $x^{2} + 2 x = 0$ C、 $x^{2} - 1 = 0$ D、 $x^{2} - 2 x + 1 = 0$

查看试题解析
5. 某校九年级（1）班部分学生上学路上所花时间如图所示.设他们上学路上所花时间的平均数为 $a$ ，中位数为 $b$ ，众数为 $c$ ，则有（）

A、 $b > a > c$ B、 $c > a > b$ C、 $a > b > c$ D、 $b > c > a$

查看试题解析
6. 如图， $A C$ 为半圆的直径，弦 $A B = 3$ ， $∠ B A C = 30 °$ ，点 $E$ 、 $F$ 分别为 $A B$ 和 $A C$ 上的动点，则 $B F + E F$ 的最小值为（）

A、 $\sqrt{3}$ B、 $\frac{3 \sqrt{3}}{2}$ C、3 D、 $\frac{3}{2} + \sqrt{3}$

查看试题解析

二、填空题

7. 方程x²﹣4＝0的解是．

查看试题解析
8. 若⊙O的半径为 $3 cm$ ，点 $A$ 与圆心 $O$ 的距离为 $4 cm$ ，则点 $A$ 与⊙O的位置关系是.

查看试题解析
9. 若关于 $x$ 的一元二次方程 $x^{2} + 4 x + k = 0$ 有两个相等的实数根，则 $k =$ .

查看试题解析
10. 某招聘考试分笔试和面试两种，其中笔试按60%、面试按40%计算加权平均数，作为总成绩.孔明笔试成绩90分，面试成绩85分，那么孔明的总成绩是分.

查看试题解析
11. 将方程 $x^{2} + 6 x - 3 = 0$ 化为 ${(x + h)}^{2} = k$ 的形式是.

查看试题解析
12. 如图，⊙O是 $△ A B C$ 的外接圆， $∠ A = 64 °$ ，则 $∠ O B C =$ °.

查看试题解析
13. 如图，在正八边形 $A B C D E F G H$ 中，连接 $A E$ 、 $A G$ ，则 $∠ E A G =$ °.

查看试题解析
14. 已知圆锥的母线长为 $8 cm$ ，侧面展开图的圆心角为 $45 °$ ，则该圆锥的侧面积为 ${cm}^{2}$ .

查看试题解析
15. 已知⊙ $O$ 的半径为 $6$ ，弦 $A B$ 长为 $6 \sqrt{2}$ ，则 $A B$ 所对的圆周角的度数为°.

查看试题解析
16. 如图，在四边形 $A B C D$ 中， $∠ B A D = ∠ C D A = 90 °$ ， $C D = 2 A B$ ，过 $A$ 、 $B$ 、 $D$ 三点的 $⊙ O$ 分别交 $B C$ 、 $C D$ 于点 $E$ 、 $F$ 下列结论：① $D F = C F$ ；② $\overset{⌢}{A B} = \overset{⌢}{B E}$ ；③ $A E = A D$ .其中所有正确结论的序号是.

查看试题解析

三、解答题

17. 解下列方程：

(1)、 $x^{2} - 10 x + 16 = 0$ ；

(2)、 $x (x - 3) = 6 - 2 x$ .

查看试题解析
18. 已知关于 $x$ 的方程 $x^{2} - m x + (m - 2) = 0$ .

(1)、求证：不论 $m$ 为何值，该方程总有两个不相等的实数根；

(2)、若方程有一个根是2，求 $m$ 的值以及方程的另一个根.

查看试题解析

19. 甲、乙两名同学本学期的五次数学测试成绩如下（单位：分）：

	第1次	第2次	第3次	第4次	第5次
甲	86	83	90	80	86
乙	78	82	84	89	92

(1)、完成下表：

	中位数	平均数	方差
甲	▲	85	▲
乙	84	85	24.8

(2)、请运用所学的统计知识，从两个不同角度评价甲、乙两人的数学成绩.

查看试题解析

20. 已知某企业2020年3月份的口罩产量是500万只，4月份的产量比3月份有所增长.5月份新冠疫情有所好转，口罩产量降为420万只.若两次产量变化的百分率相同，求这个百分率.

查看试题解析
21. 如图，在⊙O中， $A B$ 是⊙O的直径， $C D$ 是⊙O的弦， $C D ⊥ A B$ ，垂足为 $P$ .过点 $D$ 作⊙O的切线与 $A B$ 的延长线交于点 $E$ .

(1)、若 $∠ A B C = 56 °$ ，求 $∠ E$ 的度数；

(2)、若 $C D = 6$ ， $B P = 2$ ，求⊙O的半径.

查看试题解析
22. 如图，有一道长为 $10 m$ 的墙，计划用总长为 $54 m$ 的篱笆，靠墙围成由六个小长方形组成的矩形花圃 $A B C D$ .若花圃 $A B C D$ 面积为 $72 m^{2}$ ，求 $A B$ 的长.

查看试题解析
23. 如图，在⊙O中， $C$ 是 $\overset{⌢}{A B}$ 的中点，∠ACB=∠AOB.求证：四边形 $O A C B$ 是菱形.

查看试题解析
24. 如图， $P M$ 是⊙O的切线，切点是 $A$ ，点 $B$ 、 $C$ 、 $D$ 是 $⊙ O$ 上的点， $P A = P B$ .

(1)、求证： $P B$ 是⊙O的切线；

(2)、若 $∠ C = 92 °$ ， $∠ M A D = 40 °$ ，则 $∠ P =$ °.

查看试题解析
25. 商店销售某种商品，每件成本为30元.经市场调研，售价为40元时，可销售200件；售价每增加2元，销售量将减少20件.如果这种商品全部销售完，该商店可盈利2250元，那么该商品每件售价多少元？

查看试题解析
26. 如图，在矩形 $A B C D$ 中， $A B = 4$ ， $B C = 6$ . $E$ 为 $C D$ 边上的一个动点（不与 $C$ 、 $D$ 重合），⊙O是 $△ B C E$ 的外接圆.

(1)、若 $C E = 2$ ，⊙O交 $A D$ 于点 $F$ 、 $G$ .求 $F G$ 的长度；

(2)、若 $C E$ 的长度为 $m$ ，⊙O与 $A D$ 的位置关系随着 $m$ 的值变化而变化，试探索⊙O与 $A D$ 的位置关系及对应的 $m$ 的取值范围.

查看试题解析
27. 如图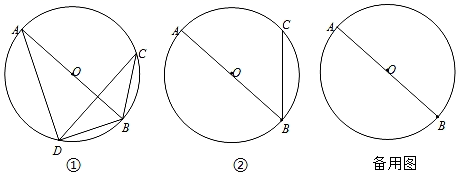

(1)、如图①，AB是⊙O的直径，C、D在⊙O上，且BC＝BD，AD＝CD.求证：∠ADC＝2∠BDC.

(2)、如图②，AB是⊙O的直径，点C在⊙O上.若平面内的点D满足AD＝CD，且∠ADC＝2∠BDC.
①利用直尺和圆规在图②中作出所有满足条件的点D（保留作图痕迹，不写作法）；

②若AB＝4，BC长度为m（0＜m＜4），则平面内满足条件的点D的个数随着m的值变化而变化，请直接写出满足条件点D的个数及对应m的取值范围.

查看试题解析