江苏省淮安市淮安区2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的是（）

A、2x+1＝0 B、x²-1＝0 C、y²+x＝1 D、 $\frac{1}{x}$ +x²＝1

查看试题解析
2. 已知⊙O的半径为2，点A与点O的距离为 $\sqrt{3}$ ，则点A与⊙O的位置关系是（）

A、点A在⊙O内 B、点A在⊙O上 C、点A在⊙O外 D、不能确定

查看试题解析
3. 判断一元二次方程 $x^{2} + 2 x - 1 = 0$ 的根的情况是（）

A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
4. 用配方法解一元二次方程x²+2x﹣3＝0时，原方程可变形为（）

A、（x+1）²＝2 B、（x+1）²＝4 C、（x+1）²＝5 D、（x+1）²＝7

查看试题解析
5. 已知三角形两边的长分别是3和6，第三边的长是方程x²﹣6x+8=0的根，则这个三角形的周长等于（）

A、13 B、11 C、11 或13 D、12或15

查看试题解析
6. 如图，四边形ABCD是⊙O的内接四边形，若∠A＝115°，则∠BOD的度数为（）

A、110° B、120° C、130° D、140°

查看试题解析
7. 以O为中心点的量角器与直角三角板ABC如图所示摆放，直角顶点B在零刻度线所在直线DE上，且量角器与三角板只有一个公共点P，∠POB＝40°，则∠CBD的度数是（）

A、50° B、45° C、35° D、40°

查看试题解析
8. 如图，AB是⊙O的直径，CD、EF是⊙O的弦，且AB∥CD∥EF.AB＝10，CD＝6，EF＝8，则图中阴影部分的面积等于（）

A、10π B、12π C、 $\frac{25 π}{2}$ D、15π

查看试题解析

二、填空题

9. 方程x²=4x的解．

查看试题解析
10. 在直径为10cm的⊙O中，弦AB=5cm，则∠AOB的度数为.

查看试题解析
11. 已知扇形的圆心角为80°，半径为3，则该扇形的弧长为（结果保留π）

查看试题解析
12. 北京奥运会的主会场“鸟巢”让人记忆深刻.在鸟巢设计的最后阶段，经过了两次优化，鸟巢的结构用钢量从5.4万吨减少到4.2万吨.若设平均每次用钢量降低的百分率为x，根据题意，可得方程

查看试题解析
13. 已知关于x的方程x²+mx﹣2＝0有一根是x＝1，则方程另一根是.

查看试题解析
14. 已知关于 $x$ 的一元二次方程 $m x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则 $m$ 的取值范围是.

查看试题解析
15. 如图，在边长为4的正方形ABCD中，以点B为圆心，以AB为半径画弧，交对角线BD于点E，则图中阴影部分的面积是（结果保留π）

查看试题解析
16. 如图，Rt△ABC的内切圆⊙I分别与斜边AB、直角边BC、CA切于点D、E、F，AD＝3，BD＝2，则Rt△ABC的面积为.

查看试题解析

三、解答题

17. 解下列方程

(1)、 $x^{2} + 2 x + 1 = 0$

(2)、 ${(x - 3)}^{2} = x - 3$

查看试题解析
18. 如图， $⊙ O$ 是 $Δ A B C$ 的外接圆，直径 $A D = 4$ ， $∠ A B C = ∠ D A C$ ，求 $A C$ 的长.

查看试题解析
19. 已知关于x的方程x²+mx+m-2=0.

(1)、若此方程的一个根为1,求m的值；

(2)、求证：不论m取何实数,此方程都有两个不相等的实数根.

查看试题解析
20. 如图，在长40m、宽22m的矩形地面内，修筑两条同样宽且垂直于矩形的边的道路，余下的部分铺上草坪（即阴影部分），要使草坪的面积达到760m² ，道路的宽应为多少米？

查看试题解析
21. 如图，在单位长度为1的正方形网格中，一段圆弧经过格点A、B、C.

(1)、画出该圆弧所在圆的圆心D的位置（不用写作法，保留作图痕迹，用水笔描清楚），并连接AD、CD.

(2)、⊙D的半径为（结果保留根号）；

(3)、若用扇形ADC围成一个圆锥的侧面，则该圆锥的底面圆半径是；

查看试题解析
22. 如图，AB是圆O的直径，AD是弦，∠DAB＝22.5°，过点D作圆O的切线DC交AB的延长线于点C.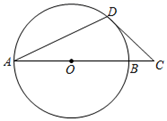

(1)、求∠C的度数；

(2)、若AB＝2 $\sqrt{2}$ ，求BC的长度.

查看试题解析
23. 如图，已知在△ABC中，∠A＝90°.

(1)、作∠ABC的角平分线交AC于点P，以点P为圆心，PA长为半径作⊙P，则⊙P与BC的位置关系是.

(2)、在（1）的条件下，若AB=3，BC=5，求⊙P的面积.

查看试题解析
24. 阅读材料：
为了解方程 ${(x^{2} - 1)}^{2} - 5 (x^{2} - 1) + 4 = 0$ ，我们可以将 $x^{2} - 1$ 视为一个整体，然后设 $x^{2} - 1 = y$ ，则原方程可化为 $y^{2} - 5 y + 4 = 0$ ①，解得 $y_{1} = 1 ， y_{2} = 4$ .

当 $y = 1$ 时， $x^{2} - 1 = 1 ， x^{2} = 2 ， ∴ x = \pm \sqrt{2}$ ；

当 $y = 4$ 时， $x^{2} - 1 = 4 ， x^{2} = 5 ， ∴ x = \pm \sqrt{5}$ .

$∴$ 原方程的解为 $x_{1} = \sqrt{2} ， x_{2} = - \sqrt{2} ， x_{3} = \sqrt{5} ， x_{4} = - \sqrt{5}$

解答问题：仿照上述方法解方程： $x^{4} - 6 x^{2} + 8 = 0$

查看试题解析
25. 如图，AB是⊙O的直径，点D在⊙O上，∠DAB=45°，BC∥AD，CD∥AB．

(1)、判断直线CD与⊙O的位置关系，并说明理由；

(2)、若⊙O的半径为1，求图中阴影部分的面积（结果保留π）

查看试题解析
26. 小丽为校合唱队购买某种服装时，商店经理给出了如下优惠条件：如果一次性购买不超过10件，单价为80元：如果一次性购买多于10件，那么每增加1件，购买的所有服装的单价降低2元，但单价不得低于50元.按此优惠条件，小丽一次性购买了这种服装x件.

(1)、填空：

购买件数x（件）

5

13

    ③

单价（元）

    ①

    ②

50

(2)、小丽一次性购买这中服装付了1200元，请问她购买了多少件这种服装？

查看试题解析
27. 问题提出：平面内不在同一条直线上的三点确定一个圆，那么平面内的四点（任意三点均不在同一直线上），能否在同一个圆上呢？
初步思考：设不在同一条直线上的三点A、B、C确定的圆为⊙O.

(1)、当C、D在线段AB的同侧时.
如图①，若点D在⊙O上，此时有∠ACB＝∠ADB，理由是.

如图②，若点D在⊙O内，此时有∠ACB ∠ADB；（填“＝”、“ $>$ ”、“ $<$ ”）

如图③，若点D在⊙O外，此时有∠ACB∠ADB；（填“＝”、“ $>$ ”、“ $<$ ”）

由上面的探究，请直接写出A、B、C、D四点在同一个圆上的条件： .

(2)、结论应用：
如图，在四边形ABCD中，连接AC，BD，∠CAD＝∠CBD＝90°，点P在CA的延长线上，连接DP.若∠ADP＝∠ABD.求证：DP为Rt△ACD的外接圆的切线.

查看试题解析

购买件数x（件）	5	13	③
单价（元）	①	②	50