江苏省常州市金坛区2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-14 类型:期中考试
一、单选题
-
1. 用配方法解一元二次方程 时,原方程可变形为( )A、 B、 C、 D、2. 关于x的方程 有两个不相等的实数根,则k的取值范围是( )A、k<1 B、k>1 C、k<-1 D、k>-13. 方程 的两根为 、 ,则 等于( )A、-6 B、6 C、-3 D、34. 下列命题:
①圆绕圆心旋转任意角度都能与自身重合;
②一个三角形只有一个内切圆;
③和半径垂直的直线是圆的切线;
④三角形的外心到三角形的三个顶点的距离相等.
其中假命题有( )
A、 个 B、 个 C、 个 D、 个5. 如图, 分别是 的直径和弦, 于点 连接 .若 ,则 的长是( )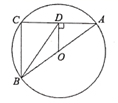 A、 B、 C、 D、6. 如图, 是 的直径, 是 的弦,且 与 交于点 ,连接 .若 则 的度数是( )
A、 B、 C、 D、6. 如图, 是 的直径, 是 的弦,且 与 交于点 ,连接 .若 则 的度数是( )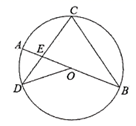 A、 B、 C、 D、7. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( )
A、 B、 C、 D、7. 如图,学校课外生物小组的试验园地的形状是长35米、宽20米的矩形.为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为600平方米,则小道的宽为多少米?若设小道的宽为 米,则根据题意,列方程为( ) A、 B、 C、 D、8. 如图,在 中,点 在弦 上移动,连接 过点 作 交 于点 .若 则 的最大值是( )
A、 B、 C、 D、8. 如图,在 中,点 在弦 上移动,连接 过点 作 交 于点 .若 则 的最大值是( )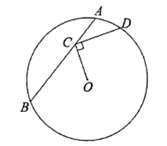 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 一元二次方程 的根是 .10. 若关于 的一元二次方程 有实根,则 的值可以是.(写出一个即可)11. 已知关于x的一元二次方程x2+kx+1=0有两个相等的实数根,则k= .
12. 某农场的粮食产量在两年内从增加 到 则平均每年增产的百分率是.13. 已知方程 有一个根是 ,则 .14. 如图, 是 的外接圆,直径 , ,则 长为.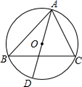 15. 如图,已知 是 的直径, 是 的切线,连接 交 于点 ,连接 .若 ,则 的度数是 .
15. 如图,已知 是 的直径, 是 的切线,连接 交 于点 ,连接 .若 ,则 的度数是 .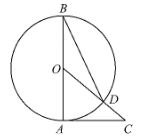 16. 若圆锥的底面半径是 圆锥的侧面积是 ,则母线长是 .17. 如图,已知点 是半圆 上一点,将弧 沿弦 折叠后恰好经过点 若半圆 的半径是 则图中阴影部分的面积是.
16. 若圆锥的底面半径是 圆锥的侧面积是 ,则母线长是 .17. 如图,已知点 是半圆 上一点,将弧 沿弦 折叠后恰好经过点 若半圆 的半径是 则图中阴影部分的面积是.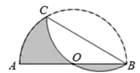 18. 如图,点 是正方形 的中心, 与 相切于点 ,连接 若 ,则 的面积是.
18. 如图,点 是正方形 的中心, 与 相切于点 ,连接 若 ,则 的面积是.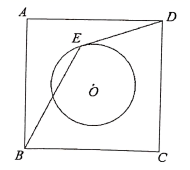
三、解答题
-
19.(1)、 ;(2)、(3)、(4)、20. 设 是一个直角三角形的两条直角边的长,且 ,求这个直角三角形的斜边长 的值.21. 某种品牌的衬衫,进货时的单价为 元.如果按每件 元销售,可销售 件;售价每提高 元,其销售量就减少 件.若要获得 元的利润,则每件的售价为多少元?22. 如图,已知 .
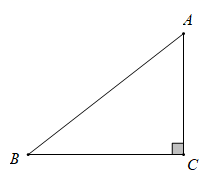 (1)、请在图中用无刻度的直尺和圆规作一个圆,使得圆心 在边 上,且与边 所在直线相切(不写作法,保留作图痕迹);(2)、在(1)的条件下,若 ,求 的半径.23. 在 中,弦 与直径 相交于点 .(1)、如图1,若 ,求 和 的大小;
(1)、请在图中用无刻度的直尺和圆规作一个圆,使得圆心 在边 上,且与边 所在直线相切(不写作法,保留作图痕迹);(2)、在(1)的条件下,若 ,求 的半径.23. 在 中,弦 与直径 相交于点 .(1)、如图1,若 ,求 和 的大小;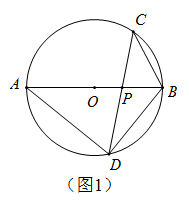 (2)、如图2,若 ,过点 作 的切线,与 的延长线相交于点 ,求 的大小.
(2)、如图2,若 ,过点 作 的切线,与 的延长线相交于点 ,求 的大小.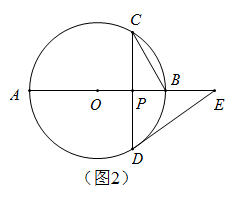 24. 已知:如图,在 中, 点 从点 出发沿 以 的速度向点 运动,同时点 从点 出发沿 以 的速度向点 运动,当点 到达终点时,点 也随即停止运动,设点 的运动时间为 .以点 为圆心, 长为半径作 .
24. 已知:如图,在 中, 点 从点 出发沿 以 的速度向点 运动,同时点 从点 出发沿 以 的速度向点 运动,当点 到达终点时,点 也随即停止运动,设点 的运动时间为 .以点 为圆心, 长为半径作 .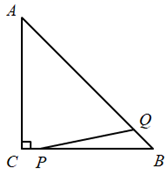 (1)、若 ,求 的值;(2)、若 与线段 有唯一公共点,求 的取值范围.25. 在平面直角坐标系 中, 的半径为 .对于图形 ,给出如下定义: 为图形 上任意一点, 为 上任意一点,如果 两点之间的距离有最大值,那么称这个最大值为图形 的“圆距”,记作 .如图,已知点 .
(1)、若 ,求 的值;(2)、若 与线段 有唯一公共点,求 的取值范围.25. 在平面直角坐标系 中, 的半径为 .对于图形 ,给出如下定义: 为图形 上任意一点, 为 上任意一点,如果 两点之间的距离有最大值,那么称这个最大值为图形 的“圆距”,记作 .如图,已知点 .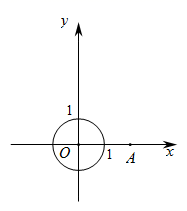 (1)、直接写出 (点 )的值;(2)、设 是直线 上一点,以为 圆心, 长为半径作 .若 满足 ,求圆心 的横坐标 的取值范围;(3)、过点 画直线 与 轴交于点 ,当 (线段 )取最小值时,直接写出 的取值范围.
(1)、直接写出 (点 )的值;(2)、设 是直线 上一点,以为 圆心, 长为半径作 .若 满足 ,求圆心 的横坐标 的取值范围;(3)、过点 画直线 与 轴交于点 ,当 (线段 )取最小值时,直接写出 的取值范围.