初中数学人教版九年级上册第二十一章一元二次方程单元检测题2

试卷更新日期：2021-09-14 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列各式 $\frac{1}{5}$ （1﹣x）=0， $\frac{4 x^{2}}{π - 3}$ =0， $\frac{x^{2} - y^{2}}{2}$ =0， $\frac{1}{x} + x = 0$ ， x²+3x=0，其中一元二次方程的个数为（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列方程中，没有实数根的是（）

A、x²-2x=0 B、x²-2x-1=0 C、x²-2x+1=0 D、x²-2x+2=0

查看试题解析
3. 下面是某同学在一次数学测验中解答的填空题，其中答对的是（）

A、若x²=4，则x=2 B、若3x²=6x，则x=2 C、x²+x-k=0的一个根是1，则k=2 D、若分式 $\frac{x (x - 2)}{x}$ 的值为零，则x=2或x=0

查看试题解析
4. 将一元二次方程5x²﹣1=4x化成一般形式后，二次项系数和一次项系数分别为（　　）

A、5，﹣4 B、5，4 C、5，1 D、5x² ， ﹣4x

查看试题解析
5. 用配方法解方程 $x^{2} + 6 x + 1 = 0$ ,配方后正确的是（）

A、 ${(x + 6)}^{2} = 35$ B、 ${(x + 6)}^{2} = 37$ C、 ${(x + 3)}^{2} = 8$ D、 ${(x + 3)}^{2} = 10$

查看试题解析
6. 已知方程x²+2x﹣3=0的解是x₁=1，x₂=﹣3，则另一个方程（x+3）²+2（x+3）﹣3=0的解是（）

A、x₁=﹣1，x₂=3 B、x₁=1，x₂=﹣3 C、x₁=2，x₂=6 D、x₁=﹣2，x₂=﹣6

查看试题解析
7. 某商场销售某品牌童装，平均每天可以售出20件，每件盈利40元，为了扩大销售，增加利润，尽量减少库存，经调查发现，每件童装每降价1元，商场平均可多销售2件．若商场每天盈利1200元，设每件童装降价x元，则可列方程（　　）

A、（20+x）（20﹣2x）=1200 B、（20﹣2x）（40+x）=1200 C、（20﹣x）（40+2x）=1200 D、（20+2x）（40﹣x）=1200

查看试题解析
8.
如图，在平行四边形ABCD中，AE⊥BC于E，AE=EB=EC=a，且a是一元二次方程x²+2x-3=0的根，则平行四边形ABCD的周长为（　　）

A、4+2 $\sqrt{2}$ B、12+6 $\sqrt{2}$ C、2+2 $\sqrt{2}$ D、2+2 $\sqrt{2}$ 或12+6 $\sqrt{2}$

查看试题解析
9. 已知关于x的方程 $x^{2} + (k^{2} - 1) x + k = 0$ 的两实数根互为相反数，则k的值等于（）

A、 $- 1$ B、1 C、1或 $- 1$ D、0

查看试题解析
10. 等腰三角形的两条边是方程x²-13x+36=0的两根，则这个三角形的周长是（）

A、17 B、22 C、13 D、17或22

查看试题解析
11. 关于x的方程ax²+bx+c=0的根为2和3，则方程ax²-bx-c=0的根（）

A、-2，-3 B、-6，1 C、2，-3 D、-1，6

查看试题解析
12. 宾馆有50间房供游客居住，当每间房每天定价为180元时，宾馆会住满；当每间房每天的定价每增加10元时，就会空闲一间房.如果有游客居住，宾馆需对居住的每间房每天支出 20元的费用.当房价定为多少元时，宾馆当天的利润为10890元？设房价比定价 180元增加 x元，则有（）

A、（x﹣20）（50﹣ $\frac{x - 180}{10}$ ）＝10890 B、x（50﹣ $\frac{x - 180}{10}$ ）﹣50×20＝10890 C、（180+x﹣20）（50﹣ $\frac{x}{10}$ ）＝10890 D、（x+180）（50﹣ $\frac{x}{10}$ ）﹣50×20＝10890

查看试题解析

二、填空题

13. 若关于x的一元二次方程（k﹣1）x²+4x+1=0有两个不相等的实数根，则k的取值范围是．

查看试题解析
14. 若关于x的一元二次方程ax²+bx+5=0（a≠0）的一个解是x=1，则2019﹣a﹣b的值是．

查看试题解析
15. x₁ ， x₂是方程x²+2x﹣3＝0的两个根，则代数式x₁²+3x₁+x₂＝．

查看试题解析
16. 若实数a、b满足a²-7a+2=0和b²-7b+2=0，则式子 $\frac{b}{a} + \frac{a}{b}$ 的值是.

查看试题解析
17. 我国南宋数学家杨辉在1275年提出了一个问题：直田积（矩形面积）八百六十四步（平方步），只云阔（宽）不及长一十二步（宽比长少一十二步）．问阔及长各几步？若设阔（宽）为x步，则所列方程为．

查看试题解析
18. 已知一元二次方程ax²+bx+c＝0（a≠0）.下列说法：①若a+c＝0，则方程一定有两个不相等的实数根；②若a+b+c＝0，则1一定是这个方程的实数根；③若b²﹣6ac＞0，则方程一定有两个不相等的实数根；④若ax²+bx+c＝0（a≠0）的两个根为2和3，则 $x_{1} = \frac{1}{2} ， x_{2} = \frac{1}{3}$ 是方cx²+bx+a＝0（a≠0）的根，其中正确的是（填序号）.

查看试题解析

三、解答题

19. 解方程

(1)、2x²+4x+1=0 （配方法）

(2)、x²+6x=5（公式法）

查看试题解析
20. 已知关于x的一元二次方程 $k x^{2} + (3 k + 1) x + 3$ =0 $(k \neq 0)$ ．
（1）求证：无论k取何值，方程总有两个实数根；
（2）若二次函数y= $k x^{2} + (3 k + 1) x + 3$ 的图象与x轴两个交点的横坐标均为整数，且k为整数，求k的值．

查看试题解析
21. 如图，要利用一面墙（墙长为25米）建羊圈，用100米的围栏围成总面积为400平方米的三个大小相同的矩形羊圈，求羊圈的边长AB，BC各为多少米？

查看试题解析
22. 如图已知直线AC的函数解析式为y= $\frac{4}{3}$ x+8，点P从点A开始沿AO方向以1个单位/秒的速度运动，点Q从O点开始沿OC方向以2个单位/秒的速度运动．如果P、Q两点分别从点A、点O同时出发，经过多少秒后能使△POQ的面积为8个平方单位？

查看试题解析
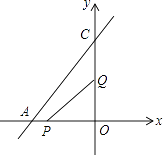23. 关于x的方程mx²﹣x﹣m+1＝0，有以下三个结论：
①当m＝0时，方程只有一个实数解；

②当m≠0时，方程有两个不相等的实数解；

③无论m取何值，方程都有一个整数根.

(1)、请你判断，这三个结论中正确的有(填序号)

(2)、证明(1)中你认为正确的结论.

查看试题解析
24. 为迎接中国森博会，某商家计划从厂家采购A，B两种产品共20件，产品的采购单价（元/件）是采购数量（件）的一次函数，下表提供了部分采购数据．
采购数量（件）
1
2
…
A产品单价（元/件）
1480
1460
…
B产品单价（元/件）
1290
1280
…

(1)、设A产品的采购数量为x（件），采购单价为y₁（元/件），求y₁与x的关系式；

(2)、经商家与厂家协商，采购A产品的数量不少于B产品数量的 $\frac{11}{9}$ ，且A产品采购单价不低于1200元，求该商家共有几种进货方案；

(3)、该商家分别以1760元/件和1700元/件的销售单价售出A，B两种产品，且全部售完，在（2）的条件下，求采购A种产品多少件时总利润最大，并求最大利润．

查看试题解析

采购数量（件）	1	2	…
A产品单价（元/件）	1480	1460	…
B产品单价（元/件）	1290	1280	…