高中数学人教A版（2019）选择性必修一立体几何与空间向量章节检测

试卷更新日期：2021-09-13 类型：单元试卷

进入出卷网下载

一、单选题

1. 已知平面 $α$ 的一个法向量 $\vec{n} = (2 ， 2 ， - 1)$ ，点 $A (0 ， 1 ， - 3)$ 在平面 $α$ 内，则点 $P (2 ， - 3 ， - 2)$ 到平面 $α$ 的距离为（）

A、 $\sqrt{3}$ B、 $\sqrt{17}$ C、 $\frac{5}{3}$ D、 $\sqrt{21}$

查看试题解析
2. 如图，在正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = A A_{1}$ ，则异面直线 $A C_{1}$ 与 $A_{1} B$ 所成角的余弦值是（）

A、0 B、 $\frac{1}{4}$ C、 $\frac{\sqrt{6}}{4}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
3. 如图，直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A C ⊥ B C ， B C = 3 ， A C = 4 ， C C_{1} = 3$ ，点P在棱 $A A_{1}$ 上，且三棱锥A-PBC的体积为4，则直线 $B C_{1}$ 与平面PBC所成角的正弦值等于（）

A、 $\frac{\sqrt{10}}{4}$ B、 $\frac{\sqrt{6}}{4}$ C、 $\frac{\sqrt{10}}{5}$ D、 $\frac{\sqrt{15}}{5}$

查看试题解析
4. 三棱锥 $S - A B C$ 中， $S A ⊥$ 底面ABC， $S A = 4$ ， $A B = 3$ ，D为AB的中点， $∠ A B C = 90 °$ ，则点D到面 $S B C$ 的距离等于（）

A、 $\frac{12}{5}$ B、 $\frac{9}{5}$ C、 $\frac{6}{5}$ D、 $\frac{3}{5}$

查看试题解析
5. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ ， $F$ ， $G$ 分别是棱 $B C$ ， $A_{1} D_{1}$ ， $B_{1} C_{1}$ 的中点，下列说法错误的是（）

A、 $E F ⊥ A G$ B、 $E F$ 与 $A G$ 是异面直线 C、 $A$ ， $E$ ， $C_{1}$ ， $F$ 四点共面 D、直线 $E C_{1}$ 与平面 $A G F$ 相交

查看试题解析
6. “阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美如图．将正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”，则异面直线AB与CD所成角的大小是（）

A、30° B、45° C、60° D、120°

查看试题解析
7. 在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $D$ 是 $B B_{1}$ 中点. $A A_{1} = 6$ ， $A C = 8$ ， $B C = 4$ ， $∠ A C B = 68 °$ .则下列结论正确的是（）

A、点 $A$ 到平面 $B C C_{1} B_{1}$ 的距离是 $4 \sqrt{3}$ B、异面直线 $D C_{1}$ 与 $A B$ 的角的余弦值是 $\frac{2}{5}$ C、若 $P$ 为侧面 $A A_{1} C_{1} C$ （含边界）上一点，满足 $B P //$ 平面 $A D C_{1}$ ，则线段 $B P$ 长的最小值是5. D、过 $A$ ， $D$ ， $C_{1}$ 的截面是钝角三角形

查看试题解析
8. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $M$ 为线段 $A_{1} D$ 的中点， $N$ 为线段 $C D_{1}$ 上的动点，则直线 $C_{1} D$ 与直线 $M N$ 所成角正弦值的最小值为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{6}}{6}$ C、 $\frac{\sqrt{6}}{3}$ D、 $\frac{\sqrt{6}}{4}$

查看试题解析

二、多选题

9. 如图，正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 的底面边长为2，侧棱长为 $2 \sqrt{3}$ ， $E$ 为 $B_{1} C_{1}$ 的中点，则正确的结论有（）

A、 $A C_{1} //$ 平面 $A_{1} B E$ B、 $A C_{1}$ 与平面 $A A_{1} B_{1} B$ 所成的角为 $\frac{π}{6}$ C、三棱锥 $A_{1} - B_{1} E B$ 的体积为 $\frac{2}{3} \sqrt{3}$ D、 $B_{1}$ 到平面 $A_{1} E B$ 的距离为 $\frac{2 \sqrt{39}}{13}$

查看试题解析
10. 正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 棱长为 $1$ ，若 $P$ 是空间异于 $C_{1}$ 的一个动点，且 $P C_{1} ⊥ B D_{1}$ ，则下列正确的是（）

A、 $P C_{1} / /$ 平面 $A C B_{1}$ B、存在唯一一点 $P$ ，使 $P D_{1} / / B_{1} C$ C、存在无数个点 $P$ ，使 $P D_{1} ⊥ B_{1} C$ D、若 $P A ⊥ P C$ ，则点 $P$ 到直线 $A_{1} C_{1}$ 的最短距离为 $\frac{\sqrt{6}}{6}$

查看试题解析
11. 某演讲比赛冠军奖杯由一个水晶球和一个金属底座组成（如图①）．已知球的体积为 $\frac{4 π}{3}$ ，金属底座是由边长为4的正三角形 $A B C$ 沿各边中点的连线向上垂直折叠而围成的几何体（如图②），则（）

A、A ，B，D，F四点共面 B、经过A，B，C三点的截面圆的面积为 $\frac{π}{4}$ C、直线 $A D$ 与平面 $D E F$ 所成的角为 $\frac{π}{3}$ D、奖杯整体高度为 $\sqrt{3} + \frac{\sqrt{6}}{3} + 1$

查看试题解析
12. 如图，在菱形 $A B C D$ 中， $A B = 2$ ， $∠ B A D = 60 °$ ，将 $△ A B D$ 沿对角线 $B D$ 翻折到 $△ C B D$ 位置，则在翻折的过程中，下列说法正确的（）

A、存在某个位置，使得 $P C = 3$ B、存在某个位置，使得 $P B ⊥ C D$ C、存在某个位置，使得 $P$ ， $B$ ， $C$ ， $D$ 四点落在半径为 $\frac{\sqrt{6}}{2}$ 的球面上 D、存在某个位置，使得点 $B$ 到平面 $P D C$ 的距离为 $\sqrt{3}$

查看试题解析

三、填空题

13. 已知 $O$ 为 $△ A B C$ 所在平面内一点，若 $(\vec{O A} + \vec{O B}) \cdot \vec{A B} = (\vec{O B} + \vec{O C}) \cdot \vec{B C} = 0$ ， $A B = 6$ ， $A C = 4$ ，则 $\vec{A O} \cdot \vec{B C} =$ .

查看试题解析
14. 在四棱锥 $S - A B C D$ 中，四边形 $A B C D$ 为正方形， $A B = 2$ ， $D S = 1$ ，平面 $A S D ⊥$ 平面 $A B C D$ ， $S D ⊥ A D$ ，点 $E$ 为 $D C$ 上的动点，平面 $B S E$ 与平面 $A S D$ 所成的二面角为 $θ$ （ $θ$ 为锐角），则当 $θ$ 取最小值时，三棱锥 $E - A S D$ 的体积为.

查看试题解析
15. 平面内一点 $P (x_{0} ， y_{0})$ 到直线 $l$ ： $A x + B y + C = 0$ 的距离为： $d = \frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ ．由此类比，空间中一点 $M (1 ， 1 ， 1)$ 到平面 $α$ ： $x + y + z + 3 = 0$ 的距离为．

查看试题解析
16. 如图，已知棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $P$ 在线段 $B_{1} C$ 上运动，给出下列结论：

①异面直线 $A P$ 与 $D D_{1}$ 所成的角范围为 $[\frac{π}{3} ， \frac{π}{2}]$ ；

②平面 $P B D_{1} ⊥$ 平面 $A_{1} C_{1} D$ ；

③点 $P$ 到平面 $A_{1} C_{1} D$ 的距离为定值 $\frac{2 \sqrt{3}}{3}$ ；

④存在一点 $P$ ，使得直线 $A P$ 与平面 $B C C_{1} B_{1}$ 所成的角为 $\frac{π}{3}$ .

其中正确的结论是.

查看试题解析

四、解答题

17. 如图，多面体 $A B C P Q$ 中， $Q A ⊥$ 平面 $A B C ， Q A / / P C$ ，点 $M$ 为 $P B$ 的中点， $A B = B C = A C = P C = 2 Q A = 2$

(1)、求证：平面 $P B Q ⊥$ 平面 $P B C$ ；

(2)、求二面角 $B - Q M - A$ 的大小.

查看试题解析
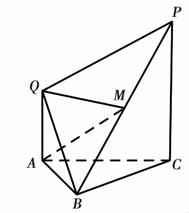18. 如图，在四棱锥P－ABCD中，△PAD为正三角形，四边形ABCD为梯形，二面角P－AD－C为直二面角，且AB∥DC，AB⊥AD，AD＝AB＝ $\frac{1}{2}$ DC，F为PC的中点.

(1)、求证：BF∥平面PAD；

(2)、求直线PC与平面PAB所成的角的余弦值.

查看试题解析
19. 在四棱锥 $P - A B C D$ 中，底面ABCD是矩形， $A B = \sqrt{2} ， A D = 2 ， E$ 为BC的中点， $P A ⊥ B C ， B D ⊥ P E$ .

(1)、证明： $P A ⊥$ 平面ABCD；

(2)、若PC与平面PAD所成的角为30°，求二面角 $A - P E - D$ 的余弦值.

查看试题解析
20. 已知四棱锥 $S - A B C D$ 中，四边形 $A B C D$ 是菱形，且 $∠ A B C = 120 °$ ， $Δ S B C$ 为等边三角形，平面 $S B C ⊥$ 平面 $A B C D$ ．

(1)、求证： $B C ⊥ S D$ ；

(2)、若点 $E$ 是线段 $S A$ 上靠近 $S$ 的三等分点，求直线 $D E$ 与平面 $S A B$ 所成角的正弦值．

查看试题解析
21. 如图，三棱锥 $P - A B C$ 的底面是等腰直角三角形，其中 $A B = A C = 2$ ， $P A = P B$ ，平面 $P A B ⊥$ 平面 $A B C$ ，点 $E$ ， $F$ ， $M$ ， $N$ 分别是 $A B$ ， $A C$ ， $P C$ ， $B C$ 的中点．

(1)、证明：平面 $E M N ⊥$ 平面 $P A B$ ；

(2)、当 $P F$ 与平面 $A B C$ 所成的角为 $\frac{π}{3}$ 时，求四棱锥 $A - P M N B$ 的体积．

查看试题解析
22. 如图，在四棱台 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，底面四边形 $A B C D$ 为菱形， $A A_{1} = A_{1} B_{1} = \frac{1}{2} A B = 1$ ， $∠ A B C = 60 °$ ， $A A_{1} ⊥$ 平面 $A B C D$ .

(1)、若点 $M$ 是 $A D$ 的中点，求证： $C_{1} M ⊥ A_{1} C$ ；

(2)、棱 $B C$ 上是否存在一点 $E$ ，使得二面角 $E - A D_{1} - D$ 的余弦值为 $\frac{1}{3}$ ？若存在，求线段 $C E$ 的长；若不存在，请说明理由.

查看试题解析