广东省深圳市光明区2022届高三上学期数学8月第一调研试卷

试卷更新日期：2021-09-13 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $A = {x | | x - 1 | < 2}$ ， $B = {x | x \leq 3 ， x \in N}$ ，则 $A \cap B =$ （）

A、 ${0 ， 1 ， 2 ， 3}$ B、 ${0 ， 1 ， 2}$ C、 ${1 ， 2 ， 3}$ D、 ${1 ， 2}$

查看试题解析
2. 已知 $z = \frac{2 - i}{2 + i}$ ，则 $\bar{z} =$ （）

A、 $\frac{4}{5} + \frac{3}{5} i$ B、 $\frac{4}{5} - \frac{3}{5} i$ C、 $\frac{3}{5} + \frac{4}{5} i$ D、 $\frac{3}{5} - \frac{4}{5} i$

查看试题解析
3. 已知圆柱的底面半径为2，侧面展开图为面积为 $8π$ 的矩形，则该圆柱的体积为（）

A、 $8π$ B、 $4π$ C、 $\frac{8}{3} π$ D、 $2 π$

查看试题解析
4. 下列区间是函数 $f (x) = 5 \cos (\frac{π}{3} - 2 x)$ 的单调递减区间的是（）

A、 $(- \frac{π}{3} ， \frac{π}{6})$ B、 $(- \frac{π}{6} ， \frac{π}{3})$ C、 $(\frac{π}{3} ， π)$ D、 $(\frac{π}{6} ， \frac{2 π}{3})$

查看试题解析
5. 已知直线l： $y = x + 1$ 与曲线C： $x^{2} + \frac{y^{2}}{2} = 1$ 相交于A ， B两点， $F (0 ， - 1)$ ，则 $△ A B F$ 的周长是（）

A、2 B、 $2 \sqrt{2}$ C、4 D、 $4 \sqrt{2}$

查看试题解析
6. 抛掷一枚质地均匀的骰子一次，记事件A为“向上的点数为奇数”，记事件B为“向上的点数为1或2”，则事件A与事件B的关系是（）

A、相互独立 B、互斥 C、既相互独立又互斥 D、既不相互独立又不互斥

查看试题解析
7. 已知函数 $f (x) = x^{2} e^{x} - 2 e x$ ，若曲线 $y = f (x)$ 在 $x = 1$ 处的切线与直线 $2 x - a y + 3 = 0$ 垂直，则 $a =$ （）

A、 $- 2 e$ B、 $- \frac{2}{e}$ C、 $\frac{e}{2}$ D、 $2 e$

查看试题解析
8. 若 $\sin (\frac{3}{4} π - x) = - 3 \sin (\frac{3}{4} π + x)$ ，则 $\frac{\sin 2 x + \sin x \cos 2 x + \sin x}{\cos^{2} \frac{x}{2}} =$ （）

A、 $\frac{4}{5}$ B、 $- \frac{4}{5}$ C、 $\frac{8}{5}$ D、 $- \frac{8}{5}$

查看试题解析

二、多选题

9. 若甲组样本数据 $x_{1}$ ， $x_{2}$ ，…， $x_{n}$ （数据各不相同）的平均数为2，方差为4，乙组样本数据 $3 x_{1} + a$ ， $3 x_{2} + a$ ，…， $3 x_{n} + a$ 的平均数为4，则下列说法正确的是（）

A、a的值为-2 B、乙组样本数据的方差为36 C、两组样本数据的样本中位数一定相同 D、两组样本数据的样本极差不同

查看试题解析
10. 已知 $\vec{e_{1}}$ ， $\vec{e_{2}}$ 是两个相互垂直的单位向量， $\vec{a} = \vec{e_{1}} - 2 \vec{e_{2}}$ ， $\vec{b} = λ \vec{e_{1}} + \vec{e_{2}}$ ，则下列说法正确的是（）

A、若 $\vec{a} // \vec{b}$ ，则 $λ = - \frac{1}{2}$ B、当 $λ = 3$ 时， $\vec{a}$ ， $\vec{b}$ 夹角的余弦值为 $\frac{\sqrt{2}}{5}$ C、存在 $λ$ 使得 $\vec{a} ⊥ \vec{b}$ 与 $| \vec{a} | = | \vec{b} |$ 同时成立 D、不论 $λ$ 为何值，总有 $| \vec{a} + \vec{b} | \geq 1$ 成立

查看试题解析
11. 过点 $P (3 ， 4)$ 作圆C： $x^{2} + y^{2} = 4$ 的两条切线，切点分别为A ， B ，则下列说法正确的是（）

A、 $| A B | = \frac{2 \sqrt{21}}{5}$ B、 $A B$ 所在直线的方程为 $3 x + 4 y - 4 = 0$ C、四边形 $P A C B$ 的外接圆方程为 $x^{2} + y^{2} - 3 x - 4 y = 0$ D、 $△ P A B$ 的面积为 $\frac{42 \sqrt{21}}{25}$

查看试题解析
12. 在棱长均为1的正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，点E在棱 $A A_{1}$ 上运动，则下列说法正确的是（）

A、 $E B + E C_{1}$ 的最小值为 $\sqrt{5}$ B、存在点E使得直线 $B E$ 与直线 $A_{1} C_{1}$ 所成的角为45° C、三棱锥 $B_{1} - E B C$ 的体积为定值 D、当点E为棱 $A A_{1}$ 的中点时，四棱锥 $E - B B_{1} C_{1} C$ 的外接球的表面积为 $\frac{25}{6} π$

查看试题解析

三、填空题

13. 已知函数 $f (x) = x^{5} (\frac{3^{x} + a}{3^{x} + 1})$ 是偶函数，则 $f (1) =$ .

查看试题解析
14. 直线 $y = k (x - 1)$ 与抛物线 $y^{2} = 4 x$ 交于A ， B两点，已知 $A B$ 的中点坐标为 $(\frac{3}{2} ， 1)$ ，则 $| A B | =$ .

查看试题解析
15. 函数 $f (x) = - 2 x - | \ln x | + 2$ 的最大值为.

查看试题解析
16. 北宋著名建筑学家李诫编写了一部记录中国古代建筑营造规范的书《营造法式》，其中说到“方一百，其斜一百四十有一”，即一个正方形的边长与它的对角线的比是 $1 ： 1.414$ ，接近 $1 ： \sqrt{2}$ .如图，该图由等腰直角三角形拼接而成，以每个等腰直角三角形斜边中点作为圆心，斜边的一半为半径作一个圆心角是90°的圆弧，所得弧线称为 $\sqrt{2}$ 螺旋线，称公比为 $\sqrt{2}$ 的数列为 $\sqrt{2}$ 等比数列.已知 $\sqrt{2}$ 等比数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，满足 $S_{n + 2} = 2 S_{n} + 2 (1 + \sqrt{2})$ .若 $b_{n} = \log_{\sqrt{2}} a_{n}$ ，且 $\sum_{i = 1}^{6} \frac{1}{4 b_{i}^{2} - 1} ⩽ 10^{λ - 5}$ ，则 $λ$ 的最小整数为.（参考数据： $\lg 2 \approx 0.3010$ ， $\lg 3 \approx 0.4771$ ）

查看试题解析

四、解答题

17. 已知数列 ${a_{n}}$ 满足 $a_{n} = [1 + {(- 1)}^{n}] \cdot 2^{n - 1}$ .

(1)、记 ${a_{n}}$ 的前n项和为 $S_{n}$ ，求 $S_{8}$ ；

(2)、记 $c_{n} = 2 n \cdot a_{n}$ ，求 ${c_{n}}$ 的前 $2 n$ 项和 $T_{2 n}$ .

查看试题解析
18. 为了不断提高群众主动参与健身的意识，激发大家的健身热情，在社区形成崇尚健身、参与健身、推动全民健身事业发展的良好氛围，某社区举行“全民健身日”活动.在活动中，甲、乙两人进行了一场五局三胜制的乒乓球比赛，其中甲在每局中胜出的概率为 $\frac{2}{3}$ ，乙在每局中胜出的概率为 $\frac{1}{3}$ ，每赢一局得1分，每输一局不得分，没有平局.每局比赛相互独立.

(1)、求甲在比赛中获胜的概率；

(2)、求比赛结束时甲得分的分布列及数学期望.

查看试题解析
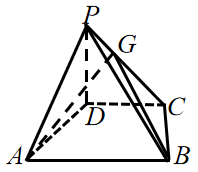19. 如图，在四棱锥 $P - A B C D$ 中， $A B // C D$ ， $A B = 2$ ， $P A = \sqrt{2}$ ， $P D ⊥ C D$ ， $A D = D C = B C = P D = 1$ .

(1)、求证： $P D ⊥ B C$ ；

(2)、在棱 $P C$ 上是否存在点G ，使得二面角 $G - A B - C$ 的大小为30°？若存在，确定点G的位置；若不存在，请说明理由.

查看试题解析
20. 在 $△ A B C$ 中，角A ， B ， C的对边分别为a ， b ， c； $3 b = 4 c$ ， $\cos C = \frac{4}{5}$ .

(1)、求 $\cos A$ 的值；

(2)、若 $△ A B C$ 的外心在其外部， $a = 7$ ，求 $△ A B C$ 外接圆的面积.

查看试题解析
21. 已知双曲线C： $\frac{x^{2}}{a^{2}} - y^{2} = 1$ （ $a > 0$ ）的左､右焦点分别为 $F_{1}$ ， $F_{2}$ ， $E (0 ， 1)$ ，过焦点 $F_{2}$ ，且斜率为 $\frac{1}{6}$ 的直线与C的两条渐近线分别交于A ， B两点，且满足 $\vec{A F_{1}} = 2 \vec{B O}$ .

(1)、求C的方程；

(2)、过点 $D (- \frac{3}{2} ， 0)$ 且斜率不为0的直线 $l_{2}$ 交C于M ， N两点，且 $| E M | = | E N |$ ，求直线 $l_{2}$ 的方程.

查看试题解析
22. 已知函数 $f (x) = \frac{1}{2} a e^{2 x} - x^{2} - a x$ ， $a \in R$ .

(1)、当 $a = 1$ 时，求函数 $g (x) = f (x) + x^{2}$ 的单调区间；

(2)、当 $0 < a < \frac{4}{e^{4} - 1}$ ，时，函数 $f (x)$ 有两个极值点 $x_{1}$ ， $x_{2}$ （ $x_{1} < x_{2}$ ），证明： $x_{2} - x_{1} > 2$ .

查看试题解析