2022届新高考一轮复习第五章三角函数的图像与性质同步练习
试卷更新日期:2021-09-12 类型:一轮复习
一、单选题
-
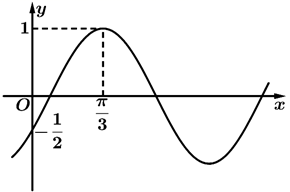
1. 若函数 的最小正周期为 ,则 ( )A、1 B、±1 C、2 D、±22. 将函数 的图象向左平移 个单位得到函数 的图象,则函数 的图象的一条对称轴方程为( )A、 B、 C、 D、3. 函数 的部分图象如图所示,要得到 的图象,只需将 的图象( )
 A、向右平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向左平移 个单位长度4. 已知当 时,函数 取得最小值,则 ( )A、 B、 C、 D、5. 已知函数 ,其图象关于点 对称且相邻两条对称轴之间的距离为 ,则下列判断正确的是 ( )A、函数 的图象关于直线 对称 B、当 时,函数 的值为 C、要得到函数 的图象,只需将 的图象向右平移 个单位 D、函数 在 上单调递增6. 把函数 图象上所有点的横坐标缩短到原来的 ,纵坐标不变,再把所得曲线向右平移 个单位长度,得到函数 的图象,则 ( )A、 B、 C、 D、7. 已知函数 的图象的一条对称轴为 ,且 ,则 的最小值为( )A、 B、 C、 D、08. 已知函数 ,其图象与直线 相邻两个交点的距离为 ,若对 ,不等式 恒成立,则 的取值范围是( )A、 B、 C、 D、
A、向右平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向左平移 个单位长度4. 已知当 时,函数 取得最小值,则 ( )A、 B、 C、 D、5. 已知函数 ,其图象关于点 对称且相邻两条对称轴之间的距离为 ,则下列判断正确的是 ( )A、函数 的图象关于直线 对称 B、当 时,函数 的值为 C、要得到函数 的图象,只需将 的图象向右平移 个单位 D、函数 在 上单调递增6. 把函数 图象上所有点的横坐标缩短到原来的 ,纵坐标不变,再把所得曲线向右平移 个单位长度,得到函数 的图象,则 ( )A、 B、 C、 D、7. 已知函数 的图象的一条对称轴为 ,且 ,则 的最小值为( )A、 B、 C、 D、08. 已知函数 ,其图象与直线 相邻两个交点的距离为 ,若对 ,不等式 恒成立,则 的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 已知函数 的部分图象如图所示,则( )
 A、 B、 C、 D、10. 已知函数 的部分自变量、函数值如下表所示,下列结论正确的是( ).
A、 B、 C、 D、10. 已知函数 的部分自变量、函数值如下表所示,下列结论正确的是( ).0
π
2π
2
5
A、函数解析式为 B、函数 图象的一条对称轴为 C、 是函数 图象的一个对称中心 D、函数 的图象左平移 个单位,再向下移2个单位所得的函数为奇函数11. 已知函数 的部分图像如图所示,则下列关于函数 的说法中正确的是( ) A、函数 最靠近原点的零点为 B、函数 的图像在 轴上的截距为 C、函数 是偶函数 D、函数 在 上单调递增12. 已知函数 ([ ]表示不超过实数 的最大整数部分),则( )A、 的最小正周期为 B、 是偶函数 C、 在 单调递减 D、 的值域为
A、函数 最靠近原点的零点为 B、函数 的图像在 轴上的截距为 C、函数 是偶函数 D、函数 在 上单调递增12. 已知函数 ([ ]表示不超过实数 的最大整数部分),则( )A、 的最小正周期为 B、 是偶函数 C、 在 单调递减 D、 的值域为三、填空题
-
13. 函数 的最小正周期 .14. 写出一个图象关于直线 对称且在 上单调递增的偶函数 .15. 若将函数 的图象向右平移 个单位长度后得到的新图象与原图象关于x轴对称,则 的最小值为.16. 关于函数 有如下四个命题:
① 的最小正周期为2;
② 的图象关于点 对称;
③若 ,则 的最小值为 ;
④ 的图象与曲线 共有4个交点.
其中所有真命题的序号是 .
四、解答题
-
17. 已知函数 .
 (1)、用五点法画出它在一个周期内的闭区间上的图象;(2)、指出 的振幅、初相、并求出对称中心.18. 已知函数 在一个周期内的图象如图所示.
(1)、用五点法画出它在一个周期内的闭区间上的图象;(2)、指出 的振幅、初相、并求出对称中心.18. 已知函数 在一个周期内的图象如图所示. (1)、求f(x)的解析式;(2)、将函数 的图象向右平移 个单位长度后,得到函数 的图象,求 在 上的单调递增区间.19. 已知函数 ,将其向右平移 个单位长度后得到函数 .(1)、求 的最小正周期和单调递减区间.(2)、若 ,求 的值域.
(1)、求f(x)的解析式;(2)、将函数 的图象向右平移 个单位长度后,得到函数 的图象,求 在 上的单调递增区间.19. 已知函数 ,将其向右平移 个单位长度后得到函数 .(1)、求 的最小正周期和单调递减区间.(2)、若 ,求 的值域.