2022届新高考一轮复习第三章基本初等函数函数同步练习
试卷更新日期:2021-09-12 类型:一轮复习
一、单选题
-
1. 定义在 上的奇函数 满足 ,则函数 的零点个数为( )A、0 B、1 C、2 D、32. 函数 在 上的零点个数为( )A、2 B、3 C、4 D、53. 函数 的零点之和为( )A、-1 B、1 C、-2 D、24. 函数 的零点所在的大致区间是( )A、 B、 C、 D、5. 已知函数 的图象与函数 的图象有唯一公共点,则实数a的值为( )A、1 B、0 C、 D、-16. 若关于 的方程 有4个不同的根,则实数 的取值范围是( )A、 B、 C、 D、7. 已知函数 若函数 有且只有1个零点,则实数a的取值范围是( )A、 B、 C、 D、8. 已知图象连续不断的函数 的定义域为R, 是周期为2的奇函数, 在区间 上恰有5个零点,则 在区间 上的零点个数为( )A、5050 B、4041 C、4040 D、2020
二、多选题
-
9. 若函数 的图像在R上连续不断,且满足 , , ,则下列说法错误的是( )A、 在区间(0,1)上一定有零点,在区间(1,2)上一定没有零点 B、 在区间(0,1)上一定没有零点,在区间(1,2)上一定有零点 C、 在区间(0,1)上一定有零点,在区间(1,2)上可能有零点 D、 在区间(0,1)上可能有零点,在区间(1,2)上一定有零点10. 已知函数 ,则下列说法正确的是( )A、 为奇函数 B、 为减函数 C、 有且只有一个零点 D、 的值域为11. 如图,函数 的图象由一条射线和抛物线的一部分构成, 的零点为 ,则( )
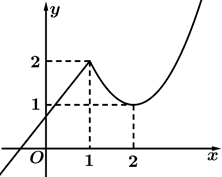 A、函数 有3个零点 B、 恒成立 C、函数 有4个零点 D、 恒成立12. 设函数 ,则下列选项正确的是( )A、 为奇函数 B、 的图象关于点 对称 C、 的最小值为 D、若 有两个不等实根,则 ,且
A、函数 有3个零点 B、 恒成立 C、函数 有4个零点 D、 恒成立12. 设函数 ,则下列选项正确的是( )A、 为奇函数 B、 的图象关于点 对称 C、 的最小值为 D、若 有两个不等实根,则 ,且三、填空题
-
13. 若二次函数 的两个零点分别是2和3,则 的值为.14. 若函数 ,则函数 的零点是.15. 已知函数 , ,若函数 有三个零点,则实数a的取值范围是.16. 同学们,你们是否注意到:自然下垂的铁链;空旷的田野上,两根电线杆之间的电线;峡谷的上空,横跨深涧的观光索道的钢索.这些现象中都有相似的曲线形态.事实上,这些曲线在数学上常常被称为悬链线.悬链线的相关理论在工程、航海、光学等方面有广泛的应用.在恰当的坐标系中,这类函数的表达式可以为 (其中 , 是非零常数,无理数 …),对于函数 以下结论正确的是 .
①如果 ,那么函数 为奇函数;
②如果 ,那么 为单调函数;
③如果 ,那么函数 没有零点;
④如果 那么函数 的最小值为2.
四、解答题
-
17. 画出函数f(x)=-x2+2x+3的图象,并根据图象回答下列问题.(1)、比较f(0),f(1),f(3)的大小;(2)、若x1<x2<1,比较f(x1)与f(x2)的大小;(3)、求函数f(x)的值域;(4)、若关于x的方程f(x)=k在[-1,2]内仅有一个实根,求k的取值范围.