山西省晋城市高平市2020-2021学年高一上学期数学期中考试试卷
试卷更新日期:2021-09-11 类型:期中考试
一、单选题
-
1. “ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件2. 下图中可以表示以x为自变量的函数图象是( )A、
 B、
B、 C、
C、 D、
D、 3. 已知集合 ,若集合 恰有8个子集,则 的取值范围是( )A、(-2,-1] B、[-2,-1) C、[-1,0) D、(-1,0]4. 已知函数 则f(f(-2))=( )A、5 B、 C、4 D、5. 下列结论正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 已知集合A={x|-2≤-x+1<3},B={x|x2-2x-3≤0},则用韦恩图表示它们之间的关系正确的是( )A、
3. 已知集合 ,若集合 恰有8个子集,则 的取值范围是( )A、(-2,-1] B、[-2,-1) C、[-1,0) D、(-1,0]4. 已知函数 则f(f(-2))=( )A、5 B、 C、4 D、5. 下列结论正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则6. 已知集合A={x|-2≤-x+1<3},B={x|x2-2x-3≤0},则用韦恩图表示它们之间的关系正确的是( )A、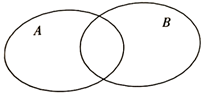 B、
B、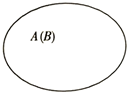 C、
C、 D、
D、 7. 若函数 在区间 内存在最小值,则 的取值范围是( )A、 B、 C、 D、8. 下列结论不正确的是( )A、“ ”是“ ”的充分不必要条件 B、“ ”是真命题 C、 内角 对边分别是 ,则“ ”是“ 是直角三角形”的充要条件 D、命题“ ”的否定是“ ”9. 已知偶函数 在 上单调递减,且 ,则不等式 的解集为( )A、 B、 C、 D、10. 已知二次函数 的图象与x轴交于 , 两点,且 ,则a的取值范围是( )A、 B、 C、 D、11. 已知实数 满足 , ,则( )A、 B、 C、 D、12. 已知 是 上的奇函数, 是 上的偶函数,且当 时, ,则( )A、 B、 C、 D、
7. 若函数 在区间 内存在最小值,则 的取值范围是( )A、 B、 C、 D、8. 下列结论不正确的是( )A、“ ”是“ ”的充分不必要条件 B、“ ”是真命题 C、 内角 对边分别是 ,则“ ”是“ 是直角三角形”的充要条件 D、命题“ ”的否定是“ ”9. 已知偶函数 在 上单调递减,且 ,则不等式 的解集为( )A、 B、 C、 D、10. 已知二次函数 的图象与x轴交于 , 两点,且 ,则a的取值范围是( )A、 B、 C、 D、11. 已知实数 满足 , ,则( )A、 B、 C、 D、12. 已知 是 上的奇函数, 是 上的偶函数,且当 时, ,则( )A、 B、 C、 D、二、填空题
-
13. 命题“∃x>1,x2-3x<0”的否定是.14. 已知集合 , ,若 ,则 .15. 已知幂函数 的图象关于 轴对称,则不等式 的解集是 .16. 已知实数 , ,且 ,则 的最小值为 .
三、解答题
-
17. 已知集合 , .(1)、用列举法表示 的全体非空子集﹔(2)、求 , .18.(1)、已知幂函数 的图象关于 轴对称,求该幂函数的解析式;(2)、已知函数 的定义域为 ,求函数 的定义域.19.(1)、用定义法证明函数 在 上单调递增;(2)、判断函数 的奇偶性,并加以证明.20. 某商品的日销售量 (单位:千克)是销售单价 (单位:元)的一次函数,且单价越高,销量越低.把销量为0时的单价称为无效价格.已知该商品的无效价格为150元,该商品的成本价是50元/千克,店主以高于成本价的价格出售该商品.(1)、若店主要获取该商品最大的日利润,则该商品的单价应定为多少元?(2)、通常情况下,获取商品最大日利润只是一种“理想结果”,如果店主要获得该商品最大日利润的64%,则该商品的单价应定为多少元?