江苏省扬州市江都区八校2020-2021学年七年级上学期数学期中联考试卷
试卷更新日期:2021-09-10 类型:期中考试
一、单选题
-
1. ﹣3的相反数为( )A、﹣3 B、﹣ C、 D、32. 下列一组数:﹣2.5,0,﹣3 , , ,0.080080008,1.121121112…其中无理数有( )A、0个 B、1个 C、2个 D、3个3. 下列各式计算正确的是( )A、 B、 C、 D、4. 已知|x|=3,|y|=2,且xy﹤0,则x+y的值等于( )A、5或-5 B、1或-1 C、5或1 D、-5或-15. 已知 ,则7﹣3m+3n的值为( )A、9 B、5 C、 D、6. 已知 有最大值,则方程 的解是
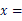 ( ) A、 B、 C、- D、-7.
( ) A、 B、 C、- D、-7.有理数a,b在数轴上的对应点如图所示,则下面式子中正确的是( )
①b<0<a; ②|b|<|a|; ③ab>0; ④a﹣b>a+b.
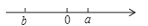 A、①② B、①④ C、②③ D、③④8. 当n≥2时,设1+2+3+…+n的末位数字为an , 比如1+2=3,末位数字为3,故a2=3,又如1+2+3+4=10,末位数字为0,故a4=0,则a2+a3+…+a888的末位数字为( )A、0 B、5 C、6 D、9
A、①② B、①④ C、②③ D、③④8. 当n≥2时,设1+2+3+…+n的末位数字为an , 比如1+2=3,末位数字为3,故a2=3,又如1+2+3+4=10,末位数字为0,故a4=0,则a2+a3+…+a888的末位数字为( )A、0 B、5 C、6 D、9二、填空题
-
9. 如果高出海平面20米,记作+20米,那么-30米表示.10. 据统计,全球每分钟约有8500000000千克污水排入江河湖海,则8500000000用科学记数法表示为.11. 单项式- 次数是.12. 若代数式 与 是同类项,那么m+n= .13. 若方程 是关于x的一元一次方程,则a等于14. 某校七年级学生乘车去郊外秋游,如果每辆汽车坐45人,那么有16人坐不上汽车;如果每辆汽车坐50人,那么有一辆汽车空出9个座位,有x辆汽车,则根据题意可列出方程为.15. 按照如图所示的计算程序,若 ,则输出的结果是.
 16. 对于任意的有理数a,b,定义新运算: , .计算:17. 若关于a,b的多项式3(a2+2ab﹣b2)﹣(a2+mab+2b2)中不含ab项,则m=.18. 已知(2x2-x-1)3=a0x6+a1x5+a2x4+a3x3+a4x2+a5x+a6 , 求a0+a2+a4=
16. 对于任意的有理数a,b,定义新运算: , .计算:17. 若关于a,b的多项式3(a2+2ab﹣b2)﹣(a2+mab+2b2)中不含ab项,则m=.18. 已知(2x2-x-1)3=a0x6+a1x5+a2x4+a3x3+a4x2+a5x+a6 , 求a0+a2+a4=三、解答题
-
19. 计算:(1)、(2)、(3)、(4)、20. 解方程:(1)、2x+4=10(2)、21. 化简(1)、-3xy-2y2+5xy-4y2(2)、2(5a2-2a)-4(-3a+2a2)22. 若(a﹣1)2+|b+2|=0,先化简:5(a2b﹣3ab2)﹣2(a2b﹣7ab2),再求值.23. 已知方程2-3(x+1)=0的解与关于x的方程 -3k-2=2x的解互为倒数,求k的值.24. 某位同学做一道题:已知两个多项式A,B,求A-B的值.他误将A-B看成A+B,求得结果为3x2-3x+5,已知B= x2-x-1.(1)、求多项式A;(2)、求A-B的正确答案.25. 有理数x , y在数轴上对应点如图所示:
 (1)、在数轴上表示﹣x , |y|;(2)、试把x , y , 0,﹣x , |y|这五个数从小到大用“<”号连接,(3)、化简:|x+y|﹣|y﹣x|+|y|.26. 甲.乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).(1)、用代数式表示(所填式子需化简):当购买乒乓球的盒数为 盒时,在甲店购买需付款元;在乙店购买需付款元.(2)、当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由.(3)、当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付款几元?27. 一般情况下 不成立,但有些数可以使得它成立,例如: .我们称使得 成立的一对数 为“相伴数对”,记为(1)、若 是“相伴数对”,求b的值;(2)、写出一个“相伴数对” ,并说明理由.(其中 ,且 )(3)、若 是“相伴数对”,求代数式 的值.28. 已知数轴上三点A,O,B对应的数分别为﹣5,0,1,点M为数轴上任意一点,其对应的数为x.请回答问题:
(1)、在数轴上表示﹣x , |y|;(2)、试把x , y , 0,﹣x , |y|这五个数从小到大用“<”号连接,(3)、化简:|x+y|﹣|y﹣x|+|y|.26. 甲.乙两家体育用品商店出售同样的乒乓球拍和乒乓球,乒乓球拍每副定价20元,乒乓球每盒定价5元.现两家商店搞促销活动,甲店的优惠办法是:每买一副乒乓球拍赠一盒乒乓球;乙店的优惠办法是:按定价的9折出售.某班需购买乒乓球拍4副,乒乓球若干盒(不少于4盒).(1)、用代数式表示(所填式子需化简):当购买乒乓球的盒数为 盒时,在甲店购买需付款元;在乙店购买需付款元.(2)、当购买乒乓球盒数为10盒时,到哪家商店购买比较合算?说出你的理由.(3)、当购买乒乓球盒数为10盒时,你能给出一种更为省钱的购买方案吗?试写出你的购买方案,并求出此时需付款几元?27. 一般情况下 不成立,但有些数可以使得它成立,例如: .我们称使得 成立的一对数 为“相伴数对”,记为(1)、若 是“相伴数对”,求b的值;(2)、写出一个“相伴数对” ,并说明理由.(其中 ,且 )(3)、若 是“相伴数对”,求代数式 的值.28. 已知数轴上三点A,O,B对应的数分别为﹣5,0,1,点M为数轴上任意一点,其对应的数为x.请回答问题: (1)、A、B两点间的距离是 , 若点M到点A、点B的距离相等,那么x的值是;(2)、有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动了2017次时,求点P所对应的有理数.(3)、当x为何值时,点M到点A、点B的距离之和是8;(4)、如果点M以每秒3个单位长度的速度从点O向左运动时,点A和点B分别以每秒1个单位长度和每秒4个单位长度的速度也向左运动,且三点同时出发,那么几秒种后点M运动到点A、点B之间,且点M到点A、点B的距离相等?
(1)、A、B两点间的距离是 , 若点M到点A、点B的距离相等,那么x的值是;(2)、有一动点P从点A出发第一次向左运动1个单位长度,然后在新的位置第二次运动,向右运动2个单位长度,在此位置第三次运动,向左运动3个单位长度…按照如此规律不断地左右运动,当运动了2017次时,求点P所对应的有理数.(3)、当x为何值时,点M到点A、点B的距离之和是8;(4)、如果点M以每秒3个单位长度的速度从点O向左运动时,点A和点B分别以每秒1个单位长度和每秒4个单位长度的速度也向左运动,且三点同时出发,那么几秒种后点M运动到点A、点B之间,且点M到点A、点B的距离相等?