江苏省盐城市响水县2020-2021学年七年级上学期数学期中考试试卷
试卷更新日期:2021-09-10 类型:期中考试
一、单选题
-
1. 下列各网格中的图形是用其图形中的一部分平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形中,由AB∥CD,能得到∠1=∠2的是A、
2. 下列计算正确的是( )A、 B、 C、 D、3. 下列图形中,由AB∥CD,能得到∠1=∠2的是A、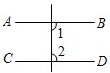 B、
B、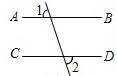 C、
C、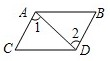 D、
D、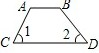 4. 下列各式中,能直接运用完全平方公式进行因式分解的是( )A、4x2+8x+1 B、x2-4x+16 C、x2-6xy-9y2 D、5. 在 ABC中,若AB=9,BC=6,则第三边CA的长度可以是( )A、3 B、6 C、15 D、166. 下列等式从左到右的变形中,是因式分解的是( )A、 B、 C、 D、7. 如图,将 ABC沿BC方向平移3cm得 DEF,若 ABC的周长为 ,则四边形ABFD的周长为( )
4. 下列各式中,能直接运用完全平方公式进行因式分解的是( )A、4x2+8x+1 B、x2-4x+16 C、x2-6xy-9y2 D、5. 在 ABC中,若AB=9,BC=6,则第三边CA的长度可以是( )A、3 B、6 C、15 D、166. 下列等式从左到右的变形中,是因式分解的是( )A、 B、 C、 D、7. 如图,将 ABC沿BC方向平移3cm得 DEF,若 ABC的周长为 ,则四边形ABFD的周长为( ) A、21cm B、24cm C、27cm D、30cm8. 对于任意的整数a、b,规定a∆b=(ab)2-a3b,则(-2)∆3的值为( )A、48 B、32 C、80 D、88
A、21cm B、24cm C、27cm D、30cm8. 对于任意的整数a、b,规定a∆b=(ab)2-a3b,则(-2)∆3的值为( )A、48 B、32 C、80 D、88二、填空题
-
9. 每到四月,许多地方杨絮、柳絮如雪花般漫天飞舞,人们不堪其扰,据测定,杨絮纤维的直径约为0.000 010 6 m,该数值用科学记数法表示为.10. 一个多边形的每一个内角为108°,则这个多边形的内角和是.11. 已知 是完全平方式,则12. 已知x+y=3,xy=-1,则x2y+xy2=.13. 若3a=5,3b=6,则3a+b=.14. 如图,AB CD,DA⊥AC垂足为A,若∠ADC=35°,则 的度数为°.
 15. 如图,在 中,D、E分别为 、 的中点,若 的面积为 ,则 的面积为.
15. 如图,在 中,D、E分别为 、 的中点,若 的面积为 ,则 的面积为.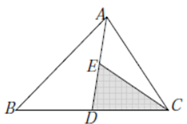 16. 如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在点A1、D1处.若∠1+∠2=130°,则∠B+∠C=°.
16. 如图,将四边形纸片ABCD沿MN折叠,点A、D分别落在点A1、D1处.若∠1+∠2=130°,则∠B+∠C=°.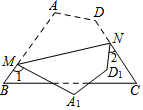
三、解答题
-
17. 计算:(1)、(2)、18. 分解因式:(1)、(2)、 .19. 先化简,再求值: ,其中 .20. 如图,在边长为1个单位的正方形网格中, ABC经过平移后得到 A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):
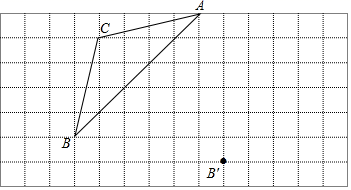
( 1 )画出 ABC的中线BD;
( 2 )画出 A′B′C′;
( 3 )连接AA′、CC′,那么线段AA′与CC′的关系是_▲_,平移过程中线段AC扫过的图形面积为▲ .
21. 完成下列证明过程,并在括号内填上依据.如图,点E在 上,点F在 上, , .求证:AB CD.

证明: (已知), ( ),
▲ (等量代换),
▲ 同位角相等,两直线平行 ,
C( ).
又 (已知),
( ),
( ).
22. 如图,DE∥BF,∠1与∠2互补.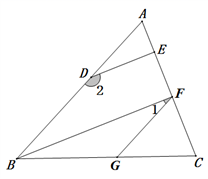 (1)、试说明:FG∥AB;(2)、若∠CFG=60°,∠2=150°,则DE与AC垂直吗?请说明理由.23. 下面是某同学对多项式 进行因式分解的过程.
(1)、试说明:FG∥AB;(2)、若∠CFG=60°,∠2=150°,则DE与AC垂直吗?请说明理由.23. 下面是某同学对多项式 进行因式分解的过程.解:设m2-4m=n,
原式=n(n+8)+16 (第一步)
=n2+8n+16 (第二步)
=(n+4)2 (第三步)
=(m2-4m+4)2(第四步)
(1)、该同学第二步到第三步运用了因式分解______.A、提取公因式 B、平方差公式 C、完全平方公式(2)、该同学是否完成了将该多项式因式分解?(填“是”或“否”).若没有完成,请直接写出因式分解的最后结果.(3)、请你模仿以上方法尝试对多项式 进行因式分解.24. (知识生成)通常情况下,通过用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.如图1,在边长为a的正方形中剪掉一个边长为b的小正方形 .把余下的部分沿虚线剪开拼成一个长方形(如图2).图1中阴影部分面积可表示为:a2-b2 , 图2中阴影部分面积可表示为(a+b)(a-b),因为两个图中的阴影部分面积是相同的,所以可得到等式:a2-b2=(a+b)(a-b);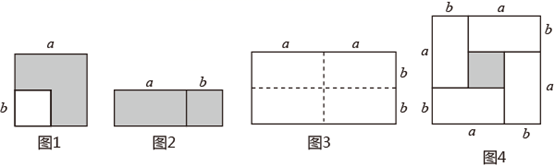
(拓展探究)图3是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图4的形状拼成一个正方形.
(1)、用两种不同方法表示图4中阴影部分面积:方法1: , 方法2:;
(2)、由(1)可得到一个关于(a+b)2、(a-b)2、ab的的等量关系式是;(3)、若a+b=10,ab=5,则(a-b)2=;(4)、(知识迁移)
如图5,将左边的几何体上下两部分剖开后正好可拼成如右图的一个长方体.根据不同方法表示它的体积也可写出一个代数恒等式:. 25. 如图1,直线m与直线n相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.
25. 如图1,直线m与直线n相交于O,点A在直线m上运动,点B 在直线n上运动,AC、BC分别是∠BAO和∠ABO的角平分线.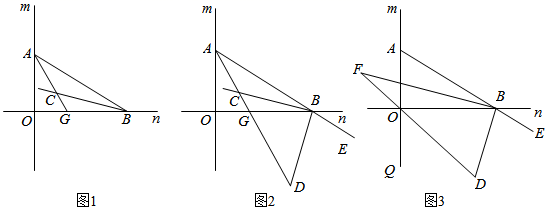 (1)、若∠BAO=50°,∠ABO=40°,求∠ACB的度数;(2)、如图2,若∠AOB=α,BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其度数(用含α的代数式表示);(3)、如图3,若直线m与直线n相互垂直,延长AB至E,已知∠ABO、∠OBE的角平分线与∠BOQ的角平分线及延长线分别相交于D、F,在△BDF中,如果有一个角是另一个角的3倍,请直接写出∠BAO的度数.
(1)、若∠BAO=50°,∠ABO=40°,求∠ACB的度数;(2)、如图2,若∠AOB=α,BD是△AOB的外角∠OBE的角平分线,BD与AC相交于点D,点A、B在运动的过程中,∠ADB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其度数(用含α的代数式表示);(3)、如图3,若直线m与直线n相互垂直,延长AB至E,已知∠ABO、∠OBE的角平分线与∠BOQ的角平分线及延长线分别相交于D、F,在△BDF中,如果有一个角是另一个角的3倍,请直接写出∠BAO的度数.