江西省九江市六校2020-2021学年高一上学期数学期中联考试卷
试卷更新日期:2021-09-10 类型:期中考试
一、单选题
-
1. 设集合 ,集合 ,则 ( )A、 B、 C、 D、2. 下列各组函数中,表示同一个函数的是( )A、 与 B、 与 C、 与 D、 与 ( 且 )3. 函数 的定义域为( )A、 B、 C、 D、4. 设函数 的零点为 ,则 所在的区间是( )A、 B、 C、 D、5. 下列在法则 的作用下,从集合 到集合 的对应中,不是映射的个数是( )
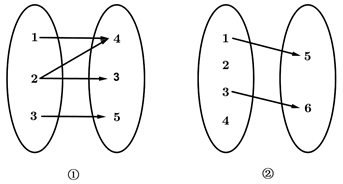
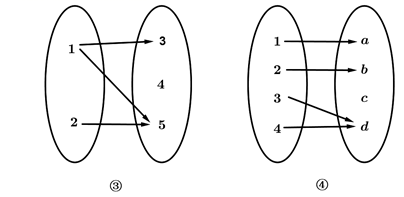 A、0 B、1 C、2 D、36. 设 , , ,则( )A、 B、 C、 D、7. 函数 的增区间是( )A、 B、 C、 D、8. 已知函数 ,那么 的值是( )A、0 B、1 C、 D、9. 函数 的图像是( )A、
A、0 B、1 C、2 D、36. 设 , , ,则( )A、 B、 C、 D、7. 函数 的增区间是( )A、 B、 C、 D、8. 已知函数 ,那么 的值是( )A、0 B、1 C、 D、9. 函数 的图像是( )A、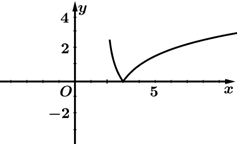 B、
B、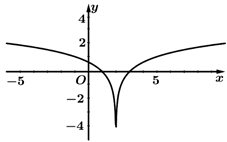 C、
C、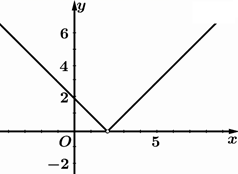 D、
D、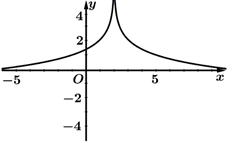 10. 已知函数 在 上的值域为 ,则实数 的取值范围是( )A、 B、 C、 D、11. 已知函数 的定义域是 ,则 的定义域为( )A、 B、 C、 D、12. 已知函数 ( 且 ),若 有最小值,则实数 的取值范围是A、 B、 C、 D、
10. 已知函数 在 上的值域为 ,则实数 的取值范围是( )A、 B、 C、 D、11. 已知函数 的定义域是 ,则 的定义域为( )A、 B、 C、 D、12. 已知函数 ( 且 ),若 有最小值,则实数 的取值范围是A、 B、 C、 D、二、填空题
-
13. 函数 ( 且 )的图像必经过点.14. 已知函数 是 上的增函数,则 的取值范围是.15. 当 时, ,则 的取值范围是.16. 函数 ,在区间 上单调递减,则实数 的取值范围是.
三、解答题
-
17. 计算下列各式的值:(1)、 ;(2)、 .18. 设全集为 ,集合 , .(1)、求 ;(2)、已知 ,若 ,求实数 的取值范围.19. 已知函数 .(1)、判断函数 在 上的单调性,并用单调性的定义加以证明;(2)、若 ,函数满足 ,求 的取值范围.20. 已知函数 .(1)、若 ,求实数 的值;(2)、求函数 的值域.21. 新冠肺炎疫情发生后,某公司生产 型抗疫商品,第一个月是为国内生产,当地政府决定对该型商品免税,该型商品出厂价为每件20元,月销售量为12万件;后来国内疫情得到有效控制,从第二个月开始,该公司为国外生产该型抗疫商品,当地政府开始对该型抗疫商品征收税率为 ( ,即销售1元要征收 元)的税,于是该型抗疫商品出厂价就上升到每件 元,预计月销售量将减少 万件.(1)、将第二个月政府对该商品征收的税 (万元)表示成 的函数,并指出这个函数的定义域;(2)、要使第二个月该公司缴纳的税额不少于1万元的前提下,又要让该公司当月获得最大销售金额, 应为多少?22. 已知函数 ,函数 有两个零点分别是 和 .(1)、若存在 ,使不等式 成立,求实数 的取值范围;(2)、记 ,若方程 有三个不同的实数解,求实数 的取值范围.