山东省烟台招远市(五四制)2020-2021学年七年级上学期数学期中试卷
试卷更新日期:2021-09-10 类型:期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列说法错误的是( )A、在角的内部,角平分线上的点到这个角两条边的距离相等 B、线段的垂直平分线上的点到这条线段的两个端点的距离相等 C、圆有无数条对称轴 D、等腰三角形的对称轴是底角的平分线所在的直线3. 已知在△ABC中,AB=8,BC=15,AC=17,则下列结论错误的是( )A、△ABC是直角三角形,且∠B=90° B、△ABC是直角三角形,且∠A=60° C、△ABC是直角三角形,且AC是它的斜边 D、△ABC的面积为604. 下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )A、
2. 下列说法错误的是( )A、在角的内部,角平分线上的点到这个角两条边的距离相等 B、线段的垂直平分线上的点到这条线段的两个端点的距离相等 C、圆有无数条对称轴 D、等腰三角形的对称轴是底角的平分线所在的直线3. 已知在△ABC中,AB=8,BC=15,AC=17,则下列结论错误的是( )A、△ABC是直角三角形,且∠B=90° B、△ABC是直角三角形,且∠A=60° C、△ABC是直角三角形,且AC是它的斜边 D、△ABC的面积为604. 下列图形中,△A′B′C′与△ABC关于直线MN成轴对称的是( )A、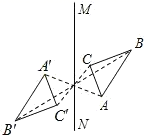 B、
B、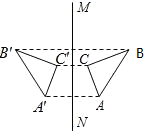 C、
C、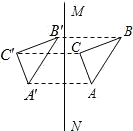 D、
D、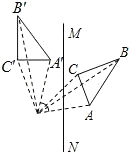 5. 如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.若AC=5,则DF=___.
5. 如图,点B、E、C、F在同一条直线上,∠A=∠D,∠B=∠DEF,BE=CF.若AC=5,则DF=___. A、10 B、6 C、5 D、26. 如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( )
A、10 B、6 C、5 D、26. 如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( ) A、CD、EF、GH B、AB、EF、GH C、AB、CD、GH D、AB、CD、EF7. 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( )
A、CD、EF、GH B、AB、EF、GH C、AB、CD、GH D、AB、CD、EF7. 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,BC为折痕,若BE是∠A′BD的平分线,则∠CBE的度数是( ) A、65度 B、115度 C、90度 D、75度8. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
A、65度 B、115度 C、90度 D、75度8. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )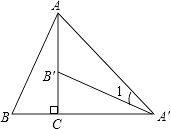 A、70° B、65° C、60° D、55°9.
A、70° B、65° C、60° D、55°9.如图,在方格纸中,以AB为一边作△ABP,使之与△ABC全等,从P1 , P2 , P3 , P4四个点中找出符合条件的点P,则点P有( )
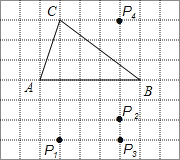 A、1个 B、2个 C、3个 D、4个10. 如图所示,正方形 和正方形 的面积分别是100和36,则以 为直径的半圆的面积是( )
A、1个 B、2个 C、3个 D、4个10. 如图所示,正方形 和正方形 的面积分别是100和36,则以 为直径的半圆的面积是( )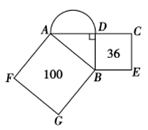 A、 B、 C、 D、11. 如图,△ABC中,AB=AC,DE是线段AB的垂直平分线,如果BD+CD=2020,那么AB的长度是( )
A、 B、 C、 D、11. 如图,△ABC中,AB=AC,DE是线段AB的垂直平分线,如果BD+CD=2020,那么AB的长度是( ) A、1010 B、2019 C、2020 D、202112. 如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为( )
A、1010 B、2019 C、2020 D、202112. 如图是一个三级台阶,它的每一级的长,宽,高分别为100cm,15cm和10cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度为( ) A、115cm B、125cm C、135cm D、145cm
A、115cm B、125cm C、135cm D、145cm二、填空题
-
13. 如图, ,要使 ,还需添加一个条件是:.(填上你认为适当的一个条件即可)
 14. 一个直角三角形的木板,三边的平方和3200,则其斜边为15. 如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,垂足为A,B,S△AOM=8cm2 , OA=4cm,则MB= .
14. 一个直角三角形的木板,三边的平方和3200,则其斜边为15. 如图,OM平分∠POQ,MA⊥OP,MB⊥OQ,垂足为A,B,S△AOM=8cm2 , OA=4cm,则MB= . 16. 如图,点E在正方形ABCD的边AB上,若EB=2,EC=5,那么正方形ABCD的面积为
16. 如图,点E在正方形ABCD的边AB上,若EB=2,EC=5,那么正方形ABCD的面积为 17. 小敏设计了一种挂衣架,在挂衣服的时候可以任意角度收扰两个挂衣杆 和 ,然后套进衣服后松开即可.如图1,衣架杆OA=OB.如图2,若衣架收拢时衣服领口宽AB=22cm,且∠AOB=60°,那么这个衣架杆的长OA=OB= .
17. 小敏设计了一种挂衣架,在挂衣服的时候可以任意角度收扰两个挂衣杆 和 ,然后套进衣服后松开即可.如图1,衣架杆OA=OB.如图2,若衣架收拢时衣服领口宽AB=22cm,且∠AOB=60°,那么这个衣架杆的长OA=OB= . 18. 七年级某班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=10cm,宽AB=8cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长度为 .
18. 七年级某班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.小明同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=10cm,宽AB=8cm的长方形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,则EC的长度为 .
三、解答题
-
19. 如图所示,在边长为1的小正方形组成的网格中,△ABC的三个顶点分别在格点上,请在网格中按要求作出下列图形,并标注相应的字母.
 (1)、作△A1B1C1 , 使得△A1B1C1 , 与△ABC关于直线l1对称;(2)、作△A2B2C2 , 使得△A2B2C2 , 与△ABC关于直线l2对称;(3)、求△A1B1C1的面积= (直接写出结果).20. 如图,AB∥FC,点E是DF的中点,若AB=20,CF=12,你能求出BD的长吗?说明理由.
(1)、作△A1B1C1 , 使得△A1B1C1 , 与△ABC关于直线l1对称;(2)、作△A2B2C2 , 使得△A2B2C2 , 与△ABC关于直线l2对称;(3)、求△A1B1C1的面积= (直接写出结果).20. 如图,AB∥FC,点E是DF的中点,若AB=20,CF=12,你能求出BD的长吗?说明理由. 21. 如图,已知△ABC中,已知 ∠B=75°, ∠C=45°,AD是BC边上的高,AE 是∠BAC的角平分线,求∠DAE的度数.
21. 如图,已知△ABC中,已知 ∠B=75°, ∠C=45°,AD是BC边上的高,AE 是∠BAC的角平分线,求∠DAE的度数. 22.
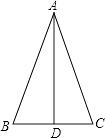
22.一如图,在△ABC中,AB=41cm,BC=18cm,BC边上的中线AD=40cm.△ABC是等腰三角形吗?为什么?
 23. 为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路 的一侧点 处有一村庄,村庄 到公路 的距离为800米,假使宣讲车 周围1000米以内能听到广播宣传,宣讲车 在公路 上沿 方向行驶时:
23. 为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路 的一侧点 处有一村庄,村庄 到公路 的距离为800米,假使宣讲车 周围1000米以内能听到广播宣传,宣讲车 在公路 上沿 方向行驶时: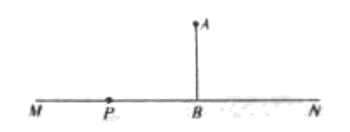 (1)、请问村庄能否听到宣传,并说明理由;(2)、如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?24. Rt△AB C中,∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).当t为何值时,△ABP为直角三角形?
(1)、请问村庄能否听到宣传,并说明理由;(2)、如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?24. Rt△AB C中,∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).当t为何值时,△ABP为直角三角形? 25. 问题情境:已知Rt△ABC的周长为56,斜边长c=25,求△ABC的面积.
25. 问题情境:已知Rt△ABC的周长为56,斜边长c=25,求△ABC的面积.解法展示:设Rt△ABC的两直角边长分别为a,b,则a+b+c= ___,
因为c=25,所以a+b=___,
所以(a+b)2=___,
所以a2+ __________=961
因为a2+b2=c2 ,
所以c2+2ab=961,
所以 _________+2ab=961,
所以ab= 168(第1步)
所以△ABC的面积= ab= × 168= 84(第2步).
合作探究:
(1)、填空:填写题目中横线处的内容.(2)、上述解题过程中,由第1步到第2步体现出来的数学思想是(填序号).①整体思想; ②数形结合思想; ③分类讨论思想.
(3)、已知一直角三角形的面积为6,斜边长为5,求这个直角三角形的周长.