江西省吉安市2020-2021学年七年级上学期数学期中试卷

试卷更新日期：2021-09-10 类型：期中考试

进入出卷网下载

一、单选题

1. $- 2$ 的相反数是（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 单项式-3πxy²z³的系数和次数分别是（　）

A、－π，5 B、－1，6 C、－3π，6　　 D、－3，7

查看试题解析
3. 下列选项中，左边的平面图形能够折成右边封闭的立体图形的是（）

A、 B、 C、 D、

查看试题解析
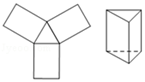4. 下列说法正确的是（）

A、最小的负整数是﹣1 B、若a+b＝0，则|a|＝|b| C、绝对值小于3的所有整数的和为3 D、有理数分为正数和负数

查看试题解析
5. 下列各组中的两项是同类项的是（）

A、 $x^{2} y$ 与 $- 2 x y^{2}$ B、 $x^{3}$ 与 $3 x$ C、 $\frac{1}{2}$ 与-1 D、 $2 x^{2} y$ 与 $- 3 x^{2} y z$

查看试题解析
6. 已知关于x的代数式﹣2x²﹣3x﹣ax²+bx+x³+1不含x的一次项和x的二次项，则a^b的值是（）

A、﹣6 B、8 C、﹣9 D、﹣8

查看试题解析

二、填空题

7. 据媒体报道，我国研制的“察打一体”无人机的速度极快，经测试最高速度可达204000米/分，将204000这个数用科学记数法表示为．

查看试题解析
8. 比较大小 $- \frac{22}{7}$ $- \frac{1}{3}$ （用“＜”或“＞”或“＝”号填空）

查看试题解析
9. 用一个平面去截五棱柱，则截面不可能是①三角形；②四边形；③五边形；④圆．（将正确的序号填上即可）

查看试题解析
10. 如图，在长为a宽为b的长方形中剪去两个半径为b的四分之一圆，用代数式表示图中阴影部分面积（用含a、b的代数式表示）．

查看试题解析
11. 已知一组代数式按如下规律排列：2x² ， ﹣4x⁴ ， 8x⁶ ， ﹣16x⁸ ， ……，则第n个代数式是（n≥1的正整数）．

查看试题解析
12. 已知：a、b互为相反数，c、d互为倒数，m的绝对值是5，则代数式2019（a+b）﹣3cd+2m的值为．

查看试题解析

三、解答题

13. 计算：

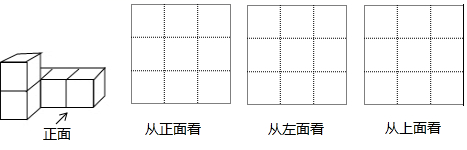
(1)、 $- 1^{2020} + | - 5 | \times (- \frac{8}{5}) - {(- 4)}^{2} \div (- 8)$ ；

(2)、4（2x²﹣y²）﹣3（3y²﹣2x²）．

查看试题解析
14. 如图所示的几何体是由5个相同的正方体搭成的，请分别画出从正面、左面、上面看到的几何体的形状图．

查看试题解析
15. 把下列各数填入相应的大括号内（将各数用逗号分开）：
﹣3，3.14， $- \frac{3}{4}$ ，0， $\frac{1}{2}$ ，0.010101…

整数：{      …}；

负数：{          …}；

正分数：{       …}．

查看试题解析
16. 气象统计资料表明，高度每增加1000米，气温就降低大约5℃，我省著名风景区庐山的最高峰高于地面约为1200米，若现在地面温度约为3℃，则山顶气温大约是多少？

查看试题解析
17. 先化简，再求值：已知A＝2a²b﹣ab² ， B＝﹣a²b+2ab² ，当a＝﹣2，b＝1时，求3A﹣2B的值．

查看试题解析
18. 如图是一个长方体纸盒的平面展开图，已知纸盒中相对两个面上的数互为相反数．

(1)、填空：a＝， b＝， c＝．

(2)、求代数式的值：a²﹣|a﹣b|+|b+c|．

查看试题解析
19. 阅读材料：我们知道，4x﹣2x+x＝（4﹣2+1）x＝3x，类似地，我们把（a+b）看成一个整体，则4（a+b）﹣2（a+b）+（a+b）＝（4﹣2+1）（a+b）＝3（a+b）．“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛尝试应用

(1)、把（a﹣b）²看成一个整体，合并3（a﹣b）²﹣6（a﹣b）²+2（a﹣b）²的结果是；

(2)、已知x²﹣2y＝4，求3x²﹣6y﹣21的值．

查看试题解析
20. 某餐厅中，一张桌子可坐6人，有以下两种摆放方式：

(1)、当有n张桌子时，两种摆放方式各能坐多少人？

(2)、一天中午餐厅要接待102位顾客共同就餐，但餐厅只有25张这样的餐桌，若你是这个餐厅的经理，你打算选择哪种方式来摆放餐桌，为什么？

查看试题解析
21. 小明帮爸爸去商城购买A品牌的茶壶和茶杯，甲、乙两家商店同时出售A品牌的茶壶和茶杯，都是茶壶每把30元，茶杯每只5元．这两家商店都有优惠，甲店买一把茶壶赠送茶杯一只；乙店全场九折优惠．小明爸爸需买茶壶5把，茶杯若干只（不少于5只）．

(1)、设购买茶杯x（x≥5）只，如果在甲店购买，需付款多少元；如果在乙店购买，需付款多少元．（用含x的代数式表示并化简）

(2)、当购买10只茶杯时，应在哪家商店购买？为什么？

查看试题解析
22. 出租车司机小王某天下午营运全是在东西走向的公路上进行的．如果向东记作“+”，向西记作“﹣”．他这天下午行车情况如下：（单位：千米；每次行车都有乘客）﹣2，+10，+1，﹣3，+2，﹣12，请回答：

(1)、小王将最后一名乘客送到目的地时，小王在出发地的什么方向？距出发地多远？

(2)、若小王的出租车每千米需油费0.4元，不计汽车的损耗，那么小王这天下午共需要多少油费？

(3)、若规定每趟车的起步价是10元，且每趟车3千米以内（含3千米）只收起步价；若超过3千米，除收起步价外，超过的部分每千米另收2元钱．那么小王这天下午收到乘客所给车费共多少元？

查看试题解析
23. 如图，在数轴上A点表示数a，B点示数b，C点表示数c，b是最小的正整数，且a，C满足 $| a + 2 | + {(c - 7)}^{2} = 0$ ．

(1)、a= ， b= ， c= ．

(2)、①若将数轴折叠，使得A点与C点重合，则点B与数表示的点重合；
②点A，B，C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动，则t秒钟时，则AC=（用含的代数式表示）．

(3)、在（2）②的条件下，请问：3BC-2AB的值是否随着时间t的变化而变化？若变化，请说明理由：若不变，请求其值．

查看试题解析