山东省潍坊市诸城市2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-09-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列说法错误的是（）

A、圆是中心对称图形，圆心就是对称中心 B、垂直于弦的直径一定平分这条弦 C、相等的弧所对的弦一定相等，反过来，相等的弦所对的弧也一定相等 D、圆是轴对称图形，任意一条通过圆心的直线都是它的对称轴

查看试题解析
2. 若锐角A满足 $\cos A = \frac{\sqrt{3}}{2}$ ，则∠A的度数为（）

A、30° B、45° C、60° D、75°

查看试题解析
3. 如图，已知 $Δ A B C$ 的六个元素，其中 $a$ 、 $b$ 、 $c$ 表示三角形三边的长，则下面甲、乙、丙、丁四个三角形中与 $Δ A B C$ 不一定相似的图形是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 在Rt△ABC中，∠C=90°，若将各边长度都扩大为原来的2倍，则∠A的正弦值（）

A、扩大2倍 B、缩小2倍 C、扩大4倍 D、不变

查看试题解析
5. 如图，⊙O的半径为5，弦AB＝8，P是弦AB上的一个动点（不与A、B重合），则OP的最小值是（）

A、2.5 B、3 C、3.5 D、4

查看试题解析
6. 如图大坝的横断面，斜坡AB的坡比i=1：2，背水坡CD的坡比i=1：1，若坡面CD的长度为 $6 \sqrt{2}$ 米，则斜坡AB的长度为（）

A、 $4 \sqrt{3}$ B、 $6 \sqrt{3}$ C、 $6 \sqrt{5}$ D、24

查看试题解析
7. 如图，ΔABC为⊙O的一个内接三角形，过点B作⊙O的切线PB与OA延长线交于点P，连接OB，已知∠P=34°，则∠ACB=（）

A、17° B、27° C、28° D、30°

查看试题解析
8. 如图，点D是△ABC的边BC上一点，∠BAD＝∠C ， AC＝2AD ，如果△ACD的面积为15，那么△ABD的面积为（）

A、15 B、10 C、7.5 D、5

查看试题解析
9. 边长为6的正三角形的外接圆的周长为（）

A、 $\sqrt{3} π$ B、 $2 \sqrt{3} π$ C、 $3 \sqrt{3} π$ D、 $4 \sqrt{3} π$

查看试题解析
10. 如图，E，F分别为矩形ABCD的边AD，BC的中点，若矩形ABCD∽矩形EABF，AB=1．求矩形ABCD的面积为（）

A、1 B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2 $\sqrt{2}$

查看试题解析
11. 如图，将矩形ABCD绕着点A逆时针旋转得到矩形AEFG，点B的对应点E落在边CD上，且DE=EF，若AD=3 $\sqrt{3}$ ，则 $\overset{⌢}{C F}$ 的长为（）

A、 $\frac{9}{4}$ π B、 $\frac{3}{4}$ π C、 $\frac{\sqrt{6}}{4}$ π D、π

查看试题解析
12. 如图，在矩形ABCD中，E是AD边的中点，BE⊥AC，垂足为点F，连接DF，下列结论：①△AEF∽△CAB；②CF=2AF；③tan∠CAD= $\sqrt{2}$ ．其中正确的结论有（）

A、3个 B、2个 C、1个 D、0个

查看试题解析

二、填空题

13. 在△ABC中，∠C＝90°，AB＝13，BC＝5，则tanB＝.

查看试题解析
14. 若△ABC∽△ADE，若AB=9，AC=8，AD=3，则EC的长是．

查看试题解析
15. 如图， $∠ A C B = 30 °$ ，点 $O$ 是 $C B$ 上的一点，且 $O C = 6$ ，则以4为半径的 $⊙ O$ 与直线 $C A$ 的公共点的个数．

查看试题解析
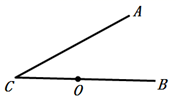16. 如图，A，B，C是⊙O上顺次三点，若AC，AB，BC分别是⊙O内接正三角形、正方形、正n边形的一边，则n= ．

查看试题解析
17. 如图，一艘船由 $A$ 港沿北偏东65°方向航行 $30 \sqrt{2} km$ 至 $B$ 港，然后再沿北偏西40°方向航行至 $C$ 港， $C$ 港在 $A$ 港北偏东20°方向，则 $A$ ， $C$ 两港之间的距离为 $km$ ．

查看试题解析
18. 如图，I是△ABC的内心，AI的延长线与△ABC的外接圆相交于点D，与BC交于点E，连接BI、CI、BD、DC．下列说法中正确的有．
①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合；

②I到△ABC三个顶点的距离相等；

③∠BIC=90°+ $\frac{1}{2}$ ∠BAC；

④点D是△BIC的外心．

查看试题解析

三、解答题

19.

(1)、计算： $\tan 45 ° - \cos 60 °$ ．

(2)、 $\sqrt{2} \sin 30 ° + \tan 60 ° - \cos 45 ° + \tan 30 °$ ．

查看试题解析
20. 如图，在平面直角坐标系中，给出了格点 $△ A B C$ （顶点均在正方形网格的格点上），已知点A的坐标为（-4，3）．

(1)、画出 $△ A B C$ 关于y轴对称的 $△ A_{1} B_{1} C_{1}$ ．

(2)、以点O为位似中心，在给定的网格中画 $△ A_{2} B_{2} C_{2}$ ，使 $△ A B C$ 与 $△ A_{2} B_{2} C_{2}$ 位似，且点 $B_{2}$ 的坐标为（2，-2）．

(3)、 $△ A B C$ 与 $△ A_{2} B_{2} C_{2}$ 的位似比是．

查看试题解析
21. 在△ABC中，∠B=45°，∠C=30°，若AB=2 $\sqrt{2}$ ，求AC的长．

查看试题解析
22. 如图所示，在平行四边形 $A B C D$ 中， $E$ 是 $C D$ 的延长线上一点， $D E = \frac{1}{2} C D$ ，连接 $B E$ 与 $A C$ ， $A D$ ， $F E$ 分别交于点 $O$ ， $F$ ．

(1)、若 $Δ D E F$ 的面积为2，求平行四边形 $A B C D$ 的面积．

(2)、求证 $O B^{2} = O E \cdot O F$ ．

查看试题解析
23. 如图，AB为⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E．

(1)、求证：BD=CD；

(2)、若AB=4，∠BAC=45°，求阴影部分的面积．

查看试题解析
24. 如图，学校操场旁立着一杆路灯（线段OP）．小明拿着一根长2m的竹竿去测量路灯的高度，他走到路灯旁的一个地点A竖起竹竿（线段AE），这时他量了一下竹竿的影长AC正好是1m，他沿着影子的方向走了4m到达点B，又竖起竹竿（线段BF），这时竹竿的影长BD正好是2m，请利用上述条件求出路灯的高度．

查看试题解析
25. 如图，四边形ABCD内接于⊙O，AB=AD，对角线BD为⊙O的直径，AC与BD交于点E．点F在CD延长线上，且DF=BC．

(1)、AC=AF；

(2)、若AD=2，AF= $\sqrt{7}$ ，求AE的长；

(3)、若EG∥CF交AF于点G，连接DG．证明：DG为⊙O的切线．

查看试题解析