山东省潍坊市寿光市2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-09-10 类型：期中考试

进入出卷网下载

一、单选题

1. 一元二次方程 $9 x^{2} = 8 x + 2$ 化为一般式后的二次项、一次项、常数项分别是（）

A、 $9 x^{2}$ ，8x，2 B、 $- 9 x^{2}$ ， $- 8 x$ ， $- 2$ C、 $9 x^{2}$ ， $- 8 x$ ， $- 2$ D、 $9 x^{2}$ ， $- 8 x$ ，2

查看试题解析
2. 若一元二次方程 $x^{2} - 2 x - 1 = 0$ 的两个根为m，n，则一次函数 $y = (m + n) x + m n$ 的图象是（）

A、 B、 C、 D、

查看试题解析
3. 电影《我和我的祖国》讲述了普通人与国家之间息息相关的动人故事.一上映就获得全国人民的追捧，第一天票房约3亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达10亿元，若把平均每天票房的增长率记作x，则可以列方程为（）

A、 $3 (1 + x) = 10$ B、 $3 {(1 + x)}^{2} = 10$ C、 $3 + 3 {(1 + x)}^{2} = 10$ D、 $3 + 3 (1 + x) + 3 {(1 + x)}^{2} = 10$

查看试题解析
4. 在Rt△ABC中，AB＝6，BC＝8，则这个三角形的内切圆的半径是（）

A、5 B、2 C、5或2 D、2或 $\sqrt{7}$ －1

查看试题解析
5. 如图，点 $A ， B ， S$ 在圆上，若弦 $A B$ 的长度等于圆半径的 $\sqrt{2}$ 倍，则 $∠ A S B$ 的度数是（）.

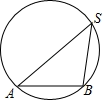A、22.5° B、30° C、45° D、60°

查看试题解析
6. 如图，为方便行人推车过天桥，市政府在10m高的天桥两端分别修建了50m长的斜道．用科学计算器计算这条斜道的倾斜角，下列按键顺序正确的是（）

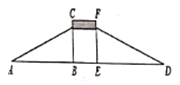A、sin0.2= B、2ndFsin0.2= C、tan0.2= D、2ndFtan0.2=

查看试题解析
7. 如图，△ABC的顶点都是正方形网格中的格点，则cos∠ACB等于（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{\sqrt{10}}{10}$

查看试题解析
8. 为了测量一个铁球的直径，将该铁球放入工件槽内，测得的有关数据如图所示（单位：cm），则该铁球的直径为（）

A、12cm B、10cm C、8cm D、6cm

查看试题解析
9. 如图，在 $Rt △ A B C$ 中， $∠ C A B = 90 °$ ， $A D ⊥ B C$ 于点D， $B D = 2$ ， $\tan ∠ C = \frac{1}{2}$ ，则线段 AC的长为（）

A、10 B、8 C、 $8 \sqrt{5}$ D、 $4 \sqrt{5}$

查看试题解析
10. 如图，⊙O与正五边形ABCDE的边AB，DE分别相切于点B，D，则劣弧BD所对的圆心角∠BOD的大小为（）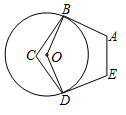

A、108° B、118° C、144° D、120°

查看试题解析
11. 如图1，在Rt△ABC中，∠B＝90°，∠ACB＝45°，延长BC到D，使CD＝AC，则tan22.5°＝（）

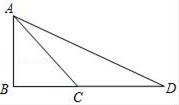A、 $\sqrt{2} + 1$ B、 $\sqrt{2} - 1$ C、 $\frac{\sqrt{2} + 1}{2}$ D、 $\frac{\sqrt{2} - 1}{2}$

查看试题解析
12.
如图，Rt△ABC中，∠ACB=90°，以AC为直径的⊙O交AB于点D，过点D作⊙O的切线，与边BC交于点E，若AD= $\frac{9}{5}$ ， AC=3．则DE长为（　　）

A、 $\frac{3}{2}$ B、2 C、 $\frac{5}{2}$ D、 $\sqrt{5}$

查看试题解析

二、填空题

13. 已知 $m$ 、 $n$ 是关于 $x$ 的一元二次方程 $x^{2} - 2 a x + a^{2} + a - 2 = 0$ 的两实根，那么 $m + n$ 的最大值是．

查看试题解析
14. 如图，⊙ $O$ 上三点 $A$ ， $B$ ， $C$ ，半径 $O C = 1$ ， $∠ A B C = 30 °$ ，⊙ $O$ 的切线 $P A$ 交 $O C$ 延长线于点 $P$ ，从现图中选取一条以P为端点的线段，此线段的长为．（注明选取的线段）

查看试题解析
15. 如图，∠EFG=90°，EF=10，OG=17，cos∠FGO=0.6，则点F的坐标是．

查看试题解析
16. 如图，在 $△ A B C$ 中，
⑴作AB和BC的垂直平分线交于点O；

⑵以点O为圆心，OA长为半径作圆；

⑶⊙O分别与AB和BC的垂直平分线交于点M，N；

⑷连接AM，AN，CM，其中AN与CM交于点P.

根据以上作图过程及所作图形，下列四个结论中，

① $\overset{⌢}{B C} = 2 \overset{⌢}{N C}$ ； ② $A B = 2 A M$ ；

③点O是 $△ A B C$ 的外心； ④点P是 $△ A B C$ 的内心.

所有正确结论的序号是.

查看试题解析
17. 如图，矩形 $A B C D$ 中， $A B = 1$ ， $B C = \sqrt{3}$ ，以 $B$ 为圆心， $B D$ 为半径画弧，交 $B C$ 延长线于 $M$ 点，以 $D$ 为圆心， $C D$ 为半径画弧，交 $A D$ 于点 $N$ ，则图中阴影部分的面积是．

查看试题解析
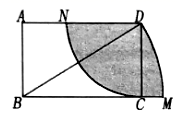18. 古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家－“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中，他觉得“有必要用几何学方式来证明曾用数字解释过的问题的符合题意性”.

以 $x^{2} + 10 x = 39$ 为例，花拉子米的几何解法如下：

如图，在边长为 $x$ 的正方形的两个相邻边上作边长分别为 $x$ 和5的矩形，再补上一个边长为5的小正方形，最终把图形补成一个大正方形.

通过不同的方式来表达大正方形的面积，可以将原方程化为（x+ ）²=39+ ，从而得到此方程的正根是 .

查看试题解析

三、解答题

19. 计算：

(1)、 $- 2^{2} + \cos 30 ° + \sin^{2} 45 ° \cos 60 ° - \sqrt{{(1 - \tan 60 °)}^{2}} - \tan 45 °$

(2)、 $3 x^{2} - 2 x - 6 = 0$

(3)、 ${(x - 1)}^{2} + 5 (x - 1) - 14 = 0$

查看试题解析
20. 我们知道 $x^{2} \geq 0$ ， ${(a \pm b)}^{2} \geq 0$ ，这一性质在数学中有着广泛的应用，比如，探究多项式 $2 x^{2} + 4 x - 5$ 的最小值时，我们可以这样处理：
解：原式 $= 2 (x^{2} + 2 x) - 5$

$= 2 (x^{2} + 2 x + 1^{2} - 1^{2}) - 5$

$= 2 [{(x + 1)}^{2} - 1^{2}] - 5$

$= 2 {(x + 1)}^{2} - 2 - 5$

$= 2 {(x + 1)}^{2} - 7$

因为 ${(x + 1)}^{2} \geq 0$ ，所以 $2 {(x + 1)}^{2} - 7 \geq 0 - 7$ ，即 $2 {(x + 1)}^{2} - 7 \geq - 7$

所以 $2 {(x + 1)}^{2} - 7$ 的最小值是 $- 7$ ，即 $2 x^{2} + 4 x - 5$ 的最小值是 $- 7$ ．

请根据上面的探究思路，解答下列问题：

(1)、多项式 $5 {(x - 3)}^{2} + 1$ 的最小值是；

(2)、求多项式 $4 x^{2} - 16 x + 3$ 的最小值（写过程）．

查看试题解析
21. 西安市某学校的数学探究小组利用无人机在操场上开展测量教学楼高度的活动，如图，此时无人机在离地面30米的点D处，操控者站在点A处，无人机测得点A的俯角为 $37 °$ ，测得教学楼楼顶点C处的俯角为 $45 °$ .又经过人工测量得到操控者和教学楼 $B C$ 的距离为57米，求教学楼BC的高度.(注：点 $A ， B ， C ， D$ 都在同一平面上，无人机大小忽略不计.参考数据： $\sin 37 ° \approx 0.60 ， \cos 37 ° \approx 0.80 ， \tan 37 ° \approx 0.75$ )

查看试题解析
22. 如图，四边形ABCD内接于⊙O，∠BAD =90°，AC是对角线．点E在BC的延长线上，且∠CED =∠BAC．

(1)、判断DE与⊙O的位置关系，并说明理由；

(2)、BA与CD的延长线交于点F，若DE∥AC，AB=4，AD =2，求AF的长．

查看试题解析
23. 已知x₁ ， x₂是关于x的一元二次方程x²＋2（m－3） x＋m²＋1＝0的两个根．

(1)、当m取何值时，方程有两个不相等的实数根？

(2)、若以x₁ ， x₂为对角线的菱形边长是 $\sqrt{3}$ ，试求m的值．

查看试题解析
24. “疫情”期间，李晨在家制作一种工艺品，并通过网络平台进行线上销售.经过一段时间后发现：当售价是40元/件时，每天可售出该商品60件，且售价每降低1元，就会多售出3件，设该商品的售价为x元/件（20≤x≤40）.

(1)、请用含售价x（元/件）的代数式表示每天能售出该工艺品的件数；

(2)、已知每件工艺品需要20元成本，每天销售该工艺品的纯利润为900元.
①求该商品的售价；

②为了支持“抗疫”行动，李晨决定每销售一件该工艺品便通过网络平台自动向某救助基金会捐款0.5元，求李晨每天通过销售该工艺品捐款的数额.

查看试题解析
25. 理解写作
如下图1，在探究锐角 $∠ A$ 的对边与直角三角形斜边之比的数学实验中包含两个环节，一是通过在 $∠ A$ 的边AB上取不同的点 $B^{'}$ ， $B^{″}$ ，分别作高 $B^{'} C^{'}$ ， $B^{″} C^{″}$ 利用三角形相似，可以说明 $\frac{B^{'} C^{'}}{A B^{'}} = \frac{B^{″} C^{″}}{A B^{″}}$ ，即 $∠ A$ 的对边与斜边的比值固定，与点 $B^{'}$ 的位置无关．

二是说明 $∠ A$ 的度数发生变化时， $∠ A$ 的对边与斜边的比值也会发生变化．请根据下图2简要说明做法并证明第二个环节的结论，并在图3中再构造一种思路证明此结论．

查看试题解析