山东省临沂市罗庄区2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-09-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 用配方法解方程x²﹣4x﹣7＝0，可变形为（）

A、（x+2）²＝3 B、（x+2）²＝11 C、（x﹣2）²＝3 D、（x﹣2）²＝11

查看试题解析
3. 如图，⊙O是正六边形ABCDEF的外接圆，点P在⊙O上（P不与A，B重合），则∠APB的度数为（）

A、60° B、60°或120° C、30° D、30°或150°

查看试题解析
4. 关于x的一元二次方程ax²+3x﹣2=0有两个不相等的实数根，则a的值可以是（）

A、0 B、﹣1 C、﹣2 D、﹣3

查看试题解析
5. 如果将抛物线y＝x²+4x+1平移，使它与抛物线y＝x²+1重合，那么平移的方式可以是（）

A、向左平移2个单位，向上平移4个单位 B、向左平移2个单位，向下平移4个单位 C、向右平移2个单位，向上平移4个单位 D、向右平移2个单位，向下平移4个单位

查看试题解析
6. 如图，圆内接四边形ABCD的两组对边的延长线分别相交于点E，F，若∠A＝55°，∠E＝30°，则∠F的度数为（）

A、25° B、30° C、40° D、55°

查看试题解析
7. 今年“十一”长假某湿地公园迎来旅游高峰，第一天的游客人数是1.2万人，第三天的游客人数为2.3万人，假设每天游客增加的百分率相同且设为x，则根据题意可列方程为（）

A、2.3 （1+x）²=1.2 B、1.2（1+x）²=2.3 C、1.2（1﹣x）²=2.3 D、1.2+1.2（1+x）+1.2（1+x）²=2.3

查看试题解析
8. 如图，已知Rt△ABC中，∠ACB=90°，AC=6，BC=4，将△ABC绕直角顶点C顺时针旋转90°得到△DEC，若点F是DE的中点，连接AF，则AF=（）

A、 $\sqrt{13}$ B、5 C、 $\sqrt{13}$ +2 D、3 $\sqrt{2}$

查看试题解析
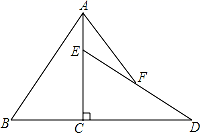9. 某校科技实践社团制作实践设备，小明的操作过程如下：①小明取出老师提供的圆形细铁环，先通过在圆一章中学到的知识找到圆心O，再任意找出圆O的一条直径标记为AB（如图1），测量出AB＝4分米；②将圆环进行翻折使点B落在圆心O的位置，翻折部分的圆环和未翻折的圆环产生交点分别标记为C、D（如图2）；③用一细橡胶棒连接C、D两点（如图3）；④计算出橡胶棒CD的长度．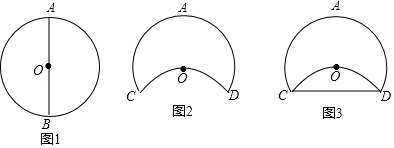

小明计算橡胶棒CD的长度为（）

A、2 $\sqrt{2}$ 分米 B、2 $\sqrt{3}$ 分米 C、3 $\sqrt{2}$ 分米 D、3 $\sqrt{3}$ 分米

查看试题解析

10. 某同学在利用描点法画二次函数y＝ax2+bx+c（a≠0）的图象时，先取自变量x的一些值，计算出相应的函数值y，如下表所示：

x	…	0	1	2	3	4	…
y	…	﹣3	0	﹣1	0	3	…

接着，他在描点时发现，表格中有一组数据计算错误，他计算错误的一组数据是（）

A、

{\begin{matrix} x = 0 \\ y = - 3 \end{matrix}

B、

{\begin{matrix} x = 2 \\ y = - 1 \end{matrix}

C、

{\begin{matrix} x = 3 \\ y = 0 \end{matrix}

D、

{\begin{matrix} x = 4 \\ y = 3 \end{matrix}

查看试题解析

11. 把一副三角板如图（1）放置，其中∠ACB＝∠DEC＝90°，∠A＝45°，∠D＝30°，斜边AB＝4，CD＝5．把三角板DCE绕着点C顺时针旋转15°得到△D₁CE₁（如图2），此时AB与CD₁交于点O，则线段AD₁的长度为（）

A、 $\sqrt{13}$ B、 $\sqrt{5}$ C、 $2 \sqrt{2}$ D、4

查看试题解析
12. 如图，一条抛物线与x轴相交于M，N两点（点M在点N的左侧），其顶点P在线段AB上移动，点A，B的坐标分别为（﹣2，﹣3），（1，﹣3），点N的横坐标的最大值为4，则点M的横坐标的最小值为（）

A、﹣1 B、﹣3 C、﹣5 D、﹣7

查看试题解析
13. 如图，在平面直角坐标系中，P是直线y＝2上的一个动点，⊙P的半径为1，直线OQ切⊙P于点Q，则线段OQ的最小值为（）

A、1 B、2 C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
14. 如图是抛物线y=ax²+bx+c（a≠0）的部分图象，其顶点是（1，n），且与x的一个交点在点（3，0）和（4，0）之间，则下列结论：①a-b+c＞0；②3a+b=0；③b²=4a（c-n）；④一元二次方程ax²+bx+c=n-1有两个不等的实数根.其中正确结论的个数是（）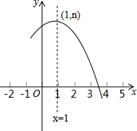

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

15. 点A（2，﹣1）关于原点对称的点B的坐标为．

查看试题解析
16. 如图，⊙O的半径为6，点A、B、C在⊙O上，且∠ACB=45°，则弦AB的长是．

查看试题解析
17. 如图，边长为2的正方形ABCD中心与半径为3的⊙O的圆心重合，E、F是AD、BA的延长线与⊙O的交点，则阴影面积是．（结果保留π）

查看试题解析
18. 如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A'B'C，M是BC的中点，N是A'B'的中点，连接MN，若BC＝4，∠ABC＝60°，则线段MN的最大值为.

查看试题解析
19. 如图，公园里喷水池中的水柱的形状可以看成是抛物线，小明想知道水柱的最大高度，于是画出示意图，并测出了一些数据：水柱上的点C，D到地面的距离都是1.6米，即 $B C = O D = 1.6$ 米， $A B = 1$ 米， $A O = 5$ 米，则水柱的最大高度是米.

查看试题解析

三、解答题

20.

(1)、x²﹣8x+1＝0；

(2)、2（x﹣2）²＝x²﹣4．

查看试题解析
21. 如图，在平面直角坐标系xOy中，点A（3，3），点B（4，0），点C（0，﹣1）．

(1)、以点C为中心，把△ABC逆时针旋转90°，画出旋转后的图形△A′B′C；

(2)、在（1）中的条件下，
①点A经过的路径 $\overset{⌢}{A A_{1}}$ 的长为（结果保留π）；

②写出点B′的坐标为．

查看试题解析
22.
某片果园有果树80棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低．若该果园每棵果树产果y（千克），增种果树x（棵），它们之间的函数关系如图所示．

(1)、求y与x之间的函数关系式；

(2)、在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实6750千克？

(3)、当增种果树多少棵时，果园的总产量w（千克）最大？最大产量是多少？

查看试题解析
23. 如图，AB为量角器（半圆O）的直径，等腰直角△BCD的斜边BD交量角器边缘于点G，直角边CD切量角器于读数为60°的点E处（即弧AE的度数为60°），第三边交量角器边缘于点F处．

(1)、求量角器在点G处的读数α（0°＜α＜90°）；

(2)、若AB＝12cm，求阴影部分面积．

查看试题解析
24. 已知△ABC是边长为4的等边三角形，边AB在射线OM上，且OA＝6，点D是射线OM上的动点，当点D不与点A重合时，将△ACD绕点C逆时针方向旋转60°得到△BCE ，连接DE ．

(1)、如图1，求证：△CDE是等边三角形．

(2)、设OD＝t ，
①当6＜t＜10时，△BDE的周长是否存在最小值？若存在，求出△BDE周长的最小值；若不存在，请说明理由．

②求t为何值时，△DEB是直角三角形（直接写出结果即可）．

查看试题解析
25. 如图，在平面直角坐标系中，直线y＝﹣x+5与y轴交于点A，与x轴交于点B．抛物线y＝﹣x²+bx+c过A、B两点．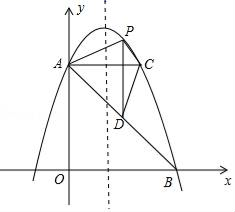

(1)、点A，B的坐标分别是A ， B ；

(2)、求抛物线的解析式；

(3)、过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的一动点（点P在AC上方），作PD平行于y轴交AB于点D，问当点P在何位置时，四边形APCD的面积最大？并求出最大面积．

查看试题解析