山东省鄄城县2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-09-10 类型：期中考试

进入出卷网下载

一、单选题

1. 若a、b、c、d是成比例线段，其中a=5cm，b=2.5cm，c=10cm，则线段d的长为（）

A、2cm B、4cm C、5cm D、6cm

查看试题解析
2. 如图，菱形ABCD中，∠B＝120°，则∠1的度数是（）

A、30° B、25° C、20° D、15°

查看试题解析
3. 用配方法解方程 $4 x^{2} - 2 x - 1 = 0$ 时，配方结果正确的是（）．

A、 ${(x - \frac{1}{2})}^{2} = \frac{1}{2}$ B、 ${(x - \frac{1}{4})}^{2} = \frac{1}{2}$ C、 ${(x - \frac{1}{4})}^{2} = \frac{3}{16}$ D、 ${(x - \frac{1}{4})}^{2} = \frac{5}{16}$

查看试题解析
4. 如图，矩形ABCD中，对角线AC＝4， △AOB 是等边三角形，则AD的长为（）

A、2 B、3 C、 $2 \sqrt{2}$ D、 $2 \sqrt{3}$

查看试题解析
5. 如图，在矩形 $A B C D$ 中，点 $E$ ， $F$ 分别是 $A D$ ， $B C$ 边的中点，连接 $E F$ ，若矩形 $A B F E$ 与矩形 $A B C D$ 相似， $A B = 1$ ，则矩形 $A B C D$ 的面积为（）

A、1 B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、 $2 \sqrt{2}$

查看试题解析
6. 关于 $x$ 的方程 $(a - 3) x^{2} - 4 x - 1 = 0$ 有两个不相等的实数根，则 $a$ 的取值范围是（）

A、 $a \geq - 1$ 且 $a \neq 3$ B、 $a > - 1$ 且 $a \neq 3$ C、 $a \geq - 1$ D、 $a > - 1$

查看试题解析
7. 小李与小陈做猜拳游戏，规定每人每次至少要出一个手指，两人出拳的手指数之和为偶数时小李获胜，那么，小李获胜的概率为（）

A、 $\frac{13}{25}$ B、 $\frac{12}{25}$ C、 $\frac{4}{25}$ D、 $\frac{1}{2}$

查看试题解析
8. 在一次数学课上，张老师出示了一个题目：“如图，▱ABCD的对角线相交于点O，过点O作EF垂直于BD交AB，CD分别于点F，E，连接DF，BE，请根据上述条件，写出一个符合题意结论．”其中四位同学写出的结论如下：
小青：OE=OF；小何：四边形DFBE是正方形；

小夏：S_{四边形AFED}=S_{四边形FBCE}；小雨：∠ACE=∠CAF，

这四位同学写出的结论中错误的是（）

A、小青 B、小何 C、小夏 D、小雨

查看试题解析

二、填空题

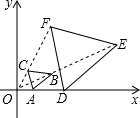
9. 在一个不透明的袋子中装有6个白球和若干个红球，这些球除颜色外都相同．每次从袋子中随机摸出一个球，记下颜色后再放回袋中，通过多次重复试验发现摸出白球的频率稳定在0.3附近，则估计袋子中的红球有个．

查看试题解析
10. 如果 $\frac{a}{b} = \frac{c}{d} = \frac{2}{3}$ ，其中 $b + 2 d \neq 0$ ，那么 $\frac{a + 2 c}{b + 2 d} =$ ．

查看试题解析
11. 如果关于x的方程（m﹣1）x³﹣mx²+2＝0是一元二次方程，那么此方程的根是．

查看试题解析
12. 如图，在平面直角坐标系中，以原点 $O$ 为位似中心，相似比为 $3 ： 1$ ，将 $Δ A B C$ 放大为 $Δ D E F$ ，已知 $C (1 ， \sqrt{2})$ ，则点 $F$ 的坐标为．

查看试题解析
13. 某公园准备围建一个矩形花园ABCD，其中一边靠墙，其他三边用长为54米的篱笆围成，已知墙EF长为28米，并且与墙平行的一面BC上要预留2米宽的入口（如图MN所示，不用围篱笆），若花园的面积为320平方米，则AB＝.

查看试题解析
14. 如图，正方形ABCD的边长是4，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值是。

查看试题解析

三、解答题

15. 解下列方程：

(1)、 $3 x^{2} - 5 x + 1 = 0$ ；

(2)、 $(x + 3) (x - 1) = 5$ ．

查看试题解析
16.
已知：如图，在矩形ABCD中，点E在边AB上，点F在边BC上，且BE=CF，EF⊥DF，求证：BF=CD．

查看试题解析
17. 已知关于x的一元二次方程 $x^{2} - 2 m x + m + 1 = 0$ 有两个相等的实数根，求代数 ${(m - 1)}^{2} + (m + 2) (m - 2)$ 的值．

查看试题解析
18. 如图，在 $△ A B C$ 中， $D$ 、 $E$ 、 $F$ 分别是 $A B$ 、 $A C$ 、 $B C$ 上的点，且 $D E // B C$ ， $E F // A B$ ， $A D ： D B = 2 ： 3$ ， $B C = 20 cm$ ，求 $B F$ 的长．

查看试题解析
19. 如图， $A C$ 、 $B D$ 交于点 $E$ ， $B C = C D$ ，且 $B D$ 平分 $∠ A B C$ ．

(1)、求证： $Δ A E B \sim Δ C E D$ ；

(2)、若 $B C = 6$ ， $E C = 3$ ， $A E = 2$ ，求 $A B$ 的长．

查看试题解析
20. 如图， $Δ A B C$ 中， $∠ B C A = 90 °$ ， $C D$ 是边 $A B$ 上的中线，分别过点 $C$ ， $D$ 作 $B A$ 和 $B C$ 的平行线，两线交于点 $E$ ，且 $D E$ 交 $A C$ 于点 $O$ ，连接 $A E$ ．

(1)、求证：四边形 $A D C E$ 是菱形；

(2)、若 $∠ B = 60 °$ ， $B C = 6$ ，求四边形 $A D C E$ 的面积．

查看试题解析
21. 在甲、乙两个不透明的口袋中，分别有4个和3个大小、材质完全相同的小球，其中甲口袋中的小球上标有数字0，1，2，3，乙口袋中的小球上分别标有数字1，2，3，先从甲口袋中随机摸出一个小球，记下数字为 $m$ ，再从乙口袋中随机摸出一个小球，记下数字为 $n$ ．

(1)、请用列表法或画树状图的方法表示出所有 $(m ， n)$ 可能的结果；

(2)、规定：若 $m ， n$ 都是方程 $x^{2} - 3 x + 2 = 0$ 的解时，则小明获胜；若 $m ， n$ 都不是方程 $x^{2} - 3 x + 2 = 0$ 的解时，则小宇获胜，问他们两人谁获胜的概率大？

查看试题解析
22. 因粤港澳大湾区和中国特色社会主义先行示范区的双重利好，深圳已成为国内外游客最喜欢的旅游目的地城市之一．深圳著名旅游“网红打卡地”东部华侨城景区在2018年春节长假期间，共接待游客达20万人次，预计在2020年春节长假期间，将接待游客达28.8万人次．

(1)、求东部华侨城景区2018至2020年春节长假期间接待游客人次的年平均增长率；

(2)、东部华侨城景区一奶茶店销售一款奶茶，每杯成本价为6元，根据销售经验，在旅游旺季，若每杯定价25元，则平均每天可销售300杯，若每杯价格降低1元，则平均每天可多销售30杯.2020年春节期间，店家决定进行降价促销活动，则当每杯售价定为多少元时，既能让顾客获得最大优惠，又可让店家在此款奶茶实现平均每天6300元的利润额？

查看试题解析
23. 已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．

(1)、求证：△ABM≌△DCM；

(2)、判断四边形MENF是什么特殊四边形，并证明你的结论；

(3)、当AD：AB=时，四边形MENF是正方形（只写结论，不需证明）．

查看试题解析
24. 类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．
原题：如图1，在平行四边形 $A B C D$ 中，点 $E$ 是 $B C$ 的中点，点 $F$ 是线段 $A E$ 上一点， $B F$ 的延长线交射线 $C D$ 于点 $G$ ．若 $\frac{A F}{E F} = 3$ ，求 $\frac{C D}{C G}$ 的值．

(1)、尝试探究
在图1中，过点 $E$ 作 $E H / / A B$ 交 $B G$ 于点 $H$ ，则 $A B$ 和 $E H$ 的数量关系是， $C G$ 和 $E H$ 的数量关系是， $\frac{C D}{C G}$ 的值是．

(2)、类比延伸
如图2，在原题的条件下，若 $\frac{A F}{E F} = m (m > 0)$ ，则 $\frac{C D}{C G}$ 的值是（用含有 $m$ 的代数式表示），试写出解答过程．

(3)、拓展迁移
如图3，梯形 $A B C D$ 中， $D C / / A B$ ，点 $E$ 是 $B C$ 的延长线上的一点， $A E$ 和 $B D$ 相交于点 $F$ ．若 $\frac{A B}{C D} = a$ ， $\frac{B C}{B E} = b$ ， $(a > 0 ， b > 0)$ ，则 $\frac{A F}{E F}$ 的值是（用含 $a$ 、 $b$ 的代数式表示）．

查看试题解析