山东省济宁市太白湖新区(北湖区2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-09-10 类型:期中考试
一、单选题
-
1. 下图是由八个相同的小正方体组合而成的几何体,其俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 在 中, , ,则 ( )A、 B、 C、 D、3. 函数 自变量的取值范围是( )A、x≥-3 B、x<3 C、x≤-3 D、x≤34. 由二次函数 ,可知( )A、其图象的开口向下 B、其图象的对称轴为直线x=-3 C、其最小值为1 D、当x<3时,y随x的增大而增大5. 如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线 (x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( )
2. 在 中, , ,则 ( )A、 B、 C、 D、3. 函数 自变量的取值范围是( )A、x≥-3 B、x<3 C、x≤-3 D、x≤34. 由二次函数 ,可知( )A、其图象的开口向下 B、其图象的对称轴为直线x=-3 C、其最小值为1 D、当x<3时,y随x的增大而增大5. 如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线 (x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( )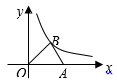 A、逐渐增大 B、不变 C、逐渐减小 D、先增大后减小6. 已知直角三角形ABC中,斜边AB的长为m,∠B=40°,则直角边BC的长是( )A、m·sin40° B、m·cos40° C、m·tan40° D、7. 设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1 , y2 , y3的大小关系为( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y3>y1>y28. 如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )
A、逐渐增大 B、不变 C、逐渐减小 D、先增大后减小6. 已知直角三角形ABC中,斜边AB的长为m,∠B=40°,则直角边BC的长是( )A、m·sin40° B、m·cos40° C、m·tan40° D、7. 设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+a上的三点,则y1 , y2 , y3的大小关系为( )A、y1>y2>y3 B、y1>y3>y2 C、y3>y2>y1 D、y3>y1>y28. 如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( ) A、 n mile B、60 n mile C、120 n mile D、 n mile9. 已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+a与反比例函数y= 在同一平面直角坐标系中的图象大致是( )
A、 n mile B、60 n mile C、120 n mile D、 n mile9. 已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+a与反比例函数y= 在同一平面直角坐标系中的图象大致是( ) A、
A、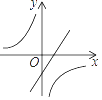 B、
B、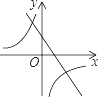 C、
C、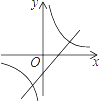 D、
D、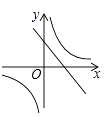 10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a、b同号;②当x =1和x=3时,函数值相等;③4a+b=0;④当-1<x<5时,y<0;⑤4a+2b>m(am+b)(m≠2的实数).其中正确的有( )
10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a、b同号;②当x =1和x=3时,函数值相等;③4a+b=0;④当-1<x<5时,y<0;⑤4a+2b>m(am+b)(m≠2的实数).其中正确的有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 将抛物线y=x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为 .12.
下面4个图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是
 13. 二次函数 (a≠0,a,b,c是常数)中,自变量x与函数y的对应值如下表:
13. 二次函数 (a≠0,a,b,c是常数)中,自变量x与函数y的对应值如下表:x
-1
-
0
1
2
3
y
-2
1
2
1
-2
一元二次方程 (a≠0,a,b,c是常数)的两个根 的取值范围是下列选项中的哪一个 (填序号)
① ②
③ ④
14. 双曲线 在第一象限的图象如图,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=3,则k的值为. 15. 规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinx•cosy+cosx•siny.
15. 规定:sin(﹣x)=﹣sinx,cos(﹣x)=cosx,sin(x+y)=sinx•cosy+cosx•siny.据此判断下列等式成立的是(写出所有正确的序号)
①cos(﹣60°)=﹣ ;
②sin75°= ;
③sin2x=2sinx•cosx;
④sin(x﹣y)=sinx•cosy﹣cosx•siny.
三、解答题
-
16. 计算:(sin30°﹣1)0﹣ sin45°+tan60°cos30°17. 同一时刻,两根木棒的影子如图,请画出图中另一根木棒的影子.
 18. 在一次篮球比赛中,如图,队员甲正在投篮.已知球出手时离地面 ,与篮圈中心的水平距离为 ,球出手后水平距离为 时达到最大高度 ,设篮球运行轨迹为抛物线,篮圈距地面 .
18. 在一次篮球比赛中,如图,队员甲正在投篮.已知球出手时离地面 ,与篮圈中心的水平距离为 ,球出手后水平距离为 时达到最大高度 ,设篮球运行轨迹为抛物线,篮圈距地面 .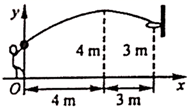 (1)、建立如图所示的平面直角坐标系,求此抛物线的解析式;(2)、此时球能否准确投中?(3)、此时,对方队员乙在甲面前 处跳起盖帽拦截,已知乙的最大摸高为 ,那么他能否获得成功?19. 自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡 米,坡度为 ;将斜坡 的高度 降低 米后,斜坡 改造为斜坡 ,其坡度为 .求斜坡 的长.(结果保留根号)
(1)、建立如图所示的平面直角坐标系,求此抛物线的解析式;(2)、此时球能否准确投中?(3)、此时,对方队员乙在甲面前 处跳起盖帽拦截,已知乙的最大摸高为 ,那么他能否获得成功?19. 自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图1所示的坡路进行改造.如图2所示,改造前的斜坡 米,坡度为 ;将斜坡 的高度 降低 米后,斜坡 改造为斜坡 ,其坡度为 .求斜坡 的长.(结果保留根号)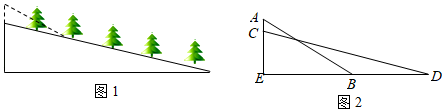 20. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.
20. 如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y= (n为常数,且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂足为D,若OB=2OA=3OD=12.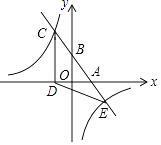 (1)、求一次函数与反比例函数的解析式;
(1)、求一次函数与反比例函数的解析式;
(2)、记两函数图象的另一个交点为E,求△CDE的面积;
(3)、直接写出不等式kx+b≤ 的解集.
21. 定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x⩾0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数。例如:一次函数y=x−1,它们的相关函数为y= .(1)、已知点A(−5,8)在一次函数y=ax−3的相关函数的图象上,求a的值;(2)、已知二次函数y=−x +4x− .①当点B(m, )在这个函数的相关函数的图象上时,求m的值;
②当−3⩽x⩽3时,求函数y=−x +4x− 的相关函数的最大值和最小值.
22. 如图抛物线过坐标原点O和x轴上另一点E,顶点M为 (2,4);矩形ABCD顶点A与点O重合,AD、AB分别在x轴、y轴上,且AD=2,AB=3. (1)、求该抛物线所对应的函数关系式;(2)、将矩形ABCD以每秒1个单位长度的速从图示位置沿x轴正方向匀速平行移动,同时一动点P也以相同速度从点A出发向B匀速移动,设它们运动时间为t秒(0≤t≤3),直线AB与该抛物线交点为N
(1)、求该抛物线所对应的函数关系式;(2)、将矩形ABCD以每秒1个单位长度的速从图示位置沿x轴正方向匀速平行移动,同时一动点P也以相同速度从点A出发向B匀速移动,设它们运动时间为t秒(0≤t≤3),直线AB与该抛物线交点为N① 当t= 时,判断点P是否在直线ME上,说明理由;
② 设以P、N、C、D为顶点的多边形面积为S,试问S是否存在最大值?说明理由.