辽宁省锦州市凌海市2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-09-10 类型:期中考试
一、单选题
-
1. 用配方法解一元二次方程x2﹣6x﹣10=0时,下列变形正确的为( )A、(x+3)2=1 B、(x﹣3)2=1 C、(x+3)2=19 D、(x﹣3)2=192. 菱形的边长是 ,一条对角线的长为 ,则另一条对角线的长为( )A、 B、 C、 D、3. 若 是关于x的一元二次方程 的一个根,则m的值为( )A、1或4 B、-1或-4 C、-1或4 D、1或-44. 如图①所示,平整的地面上有一个不规则的图案(图中阴影部分),小雅想了解该图案的面积是多少,她采取了以下的办法:用一个长为 ,宽为 的长方形,将不规则图案围起来,然后在适当位置随机地向长方形区域扔小球,并记录小球在不规则图案上的次数(球扔在界线上或长方形区域外不计入试验结果),她将若干次有效试验的结果绘制成了图②所示的折线统计图,由此她估计此不规则图案的面积大约为( )
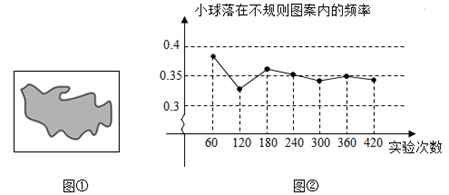 A、 B、 C、 D、5. 为增强学生身体素质,提高学生足球运动竞技水平,某校组织全校学生进行足球比赛,以班级为单位,每两个班级之间都比赛一场.现计划安排21场比赛,应邀请参赛的班级有( )A、6个 B、7个 C、8个 D、9个6. 在大量重复试验中,关于随机事件发生的频率和概率,下列说法正确的是( )A、频率就是概率 B、频率与试验次数无关 C、在相同的条件下进行试验,如果试验次数相同,则各实验小组所得频率的值也会相同 D、随着试验次数的增加,频率一般会逐步稳定在概率数值附近7. 如图,平行四边形 的对角线 与 相交于点O,添加一个条件不能使平行四边形 变为矩形的是( )
A、 B、 C、 D、5. 为增强学生身体素质,提高学生足球运动竞技水平,某校组织全校学生进行足球比赛,以班级为单位,每两个班级之间都比赛一场.现计划安排21场比赛,应邀请参赛的班级有( )A、6个 B、7个 C、8个 D、9个6. 在大量重复试验中,关于随机事件发生的频率和概率,下列说法正确的是( )A、频率就是概率 B、频率与试验次数无关 C、在相同的条件下进行试验,如果试验次数相同,则各实验小组所得频率的值也会相同 D、随着试验次数的增加,频率一般会逐步稳定在概率数值附近7. 如图,平行四边形 的对角线 与 相交于点O,添加一个条件不能使平行四边形 变为矩形的是( )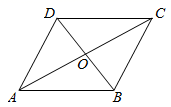 A、 B、 C、 D、8. 盈盈和同学们做“抛掷质地均匀的硬币”试验,获得的数据如下表:
A、 B、 C、 D、8. 盈盈和同学们做“抛掷质地均匀的硬币”试验,获得的数据如下表:抛掷次数
100
200
400
500
1000
正面朝上的频数
53
99
201
247
502
若抛掷硬币的次数为2000,则“正面朝上”的频数最接近( )
A、100 B、500 C、800 D、1000二、填空题
-
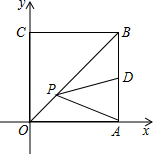
9. 已知关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是 .10. 已知 是一元二次方程 的一个根,则 的值为 .11. 从一个不透明的口袋中随机摸出一球,再放回袋中,不断重复上述过程,一共摸了150次,其中有50次摸到黑球,已知囗袋中仅有黑球10个和白球若干个,这些球除颜色外,其他都一样,由此估计口袋中有个白球.12. 某种植基地2018年蔬菜产量为100吨,预计2020年蔬菜产量将达到144吨.设蔬菜产量平均每年增长的百分率为x,根据题意可列方程为.13. 如图,在平面直角坐标系中,点A、C分别在x轴、y轴上,四边形 是边长为2的正方形,点D为 的中点,点P为 上的一个动点,连接 、 ,当点P满足 的值最小时,则点P的坐标为 .
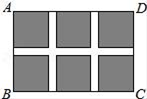
 14. 如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从F出口落出的概率是 .
14. 如图,小球从A入口往下落,在每个交叉口都有向左或向右两种可能,且可能性相等,则小球从F出口落出的概率是 .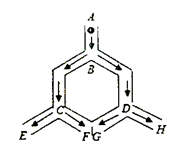 15. 如图,菱形 的边长为2, ,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于点M、N两点,直线 交 于点E,连接 ,则 的长为 .
15. 如图,菱形 的边长为2, ,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于点M、N两点,直线 交 于点E,连接 ,则 的长为 . 16. 如图,矩形 中, , , 为 的中点, 为 上一点,将 沿 折叠后,点 恰好落到 上的点 处,则折痕 的长是.
16. 如图,矩形 中, , , 为 的中点, 为 上一点,将 沿 折叠后,点 恰好落到 上的点 处,则折痕 的长是.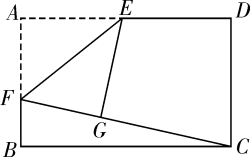
三、解答题
-
17. 用适当的方法解方程:18. 已知关于x的一元二次方程ax2+bx+1=0(a≠0)有两个相等的实数根,求 的值.19. 某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:(1)、该顾客至少可得元购物券,至多可得元购物券;(2)、请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.20. 如图,某小区规划在一个长30m、宽20m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草.要使每一块花草的面积都为78m2 , 那么通道的宽应设计成多少m?
 21. 某水果超市以每千克20元的价格购进一批大枣,规定每千克大枣的售价不低于进价又不高于40元.经市场调查发现:大枣的日销售量y(千克)与每千克售价x(元)之间满足一次函数关系,其部分对应数据如下表所示:
21. 某水果超市以每千克20元的价格购进一批大枣,规定每千克大枣的售价不低于进价又不高于40元.经市场调查发现:大枣的日销售量y(千克)与每千克售价x(元)之间满足一次函数关系,其部分对应数据如下表所示:每千克售价x(元)
…
25
30
35
…
日销售量y(千克)
…
110
100
90
…
(1)、求y与x之间的函数关系式;(2)、该水果超市想要获利1000元的日销售利润,每千克大枣的售价应定为多少元?22. 如图,已知正方形ABCD的边长为1,正方形CEFG的面积为 ,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为 ,且 .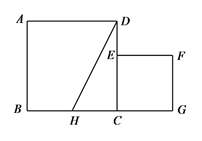 (1)、求线段CE的长;(2)、若点H为BC边的中点,连结HD,求证: .23. 如图,菱形 中,E是 的中点,将 沿 折叠后,点A和点D恰好重合,若菱形 的面积为 ,求菱形 的周长.
(1)、求线段CE的长;(2)、若点H为BC边的中点,连结HD,求证: .23. 如图,菱形 中,E是 的中点,将 沿 折叠后,点A和点D恰好重合,若菱形 的面积为 ,求菱形 的周长.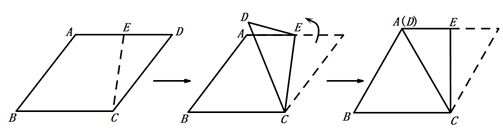 24. 如图,矩形 中,点E在边 上,将 沿 折叠,点C落在 边上的点F处,过点F作 交 于点G,连接 .
24. 如图,矩形 中,点E在边 上,将 沿 折叠,点C落在 边上的点F处,过点F作 交 于点G,连接 .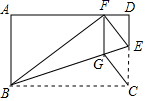 (1)、求证:四边形 是菱形;(2)、若 , ,求四边形 的面积.25. 如图,在Rt△ABC中, 现在有一足够大的直角三角板,它的直角顶点D是BC边上一点,另两条直角边分别交AB、AC于点E、F.
(1)、求证:四边形 是菱形;(2)、若 , ,求四边形 的面积.25. 如图,在Rt△ABC中, 现在有一足够大的直角三角板,它的直角顶点D是BC边上一点,另两条直角边分别交AB、AC于点E、F.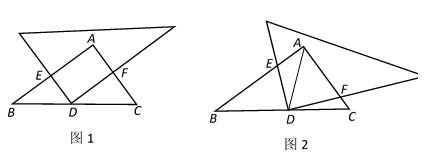 (1)、如图1,若DE⊥AB,DF⊥AC,求证:四边形AEDF是矩形(2)、在(1)条件下,若点D在∠BAC的角平分线上,试判断此时四边形AEDF形状,并说明理由;(3)、若点D在∠BAC的角平分线上,将直角三角板绕点D旋转一定的角度,使得直角三角板的两条边与两条直角边分别交于点E、F(如图2),试证明 .(尝试作辅助线)
(1)、如图1,若DE⊥AB,DF⊥AC,求证:四边形AEDF是矩形(2)、在(1)条件下,若点D在∠BAC的角平分线上,试判断此时四边形AEDF形状,并说明理由;(3)、若点D在∠BAC的角平分线上,将直角三角板绕点D旋转一定的角度,使得直角三角板的两条边与两条直角边分别交于点E、F(如图2),试证明 .(尝试作辅助线)