辽宁省锦州市黑山县2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-09-10 类型:期中考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、 C、 D、2. 方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定3. 正方形具有而菱形不具有的性质是( )A、两组对边分别平行且相等 B、两组对角分别相等 C、相邻两角互补 D、对角线相等4. 用配方法解方程 ,正确的是( )A、 B、 C、 D、5. 如图,矩形ABCD的对角线交于点O,若∠BAO=55°,则∠AOD等于( )
 A、105° B、110° C、115° D、120°6. 根据下列表格的对应值:
A、105° B、110° C、115° D、120°6. 根据下列表格的对应值:…
5.17
5.18
5.19
5.2
…
…
-0.03
-0.01
0.01
0.04
…
判断方程 ( , 、 、 为常数)一个解 的取值范围是( )
A、 B、 C、 D、7. 如果关于 的一元二次方程 有两个不相等的实数根,则 满足的条件是( )A、 B、 且 C、 且 D、8. 如图,在 中, , , 分别是 , 的中点,延长 至点 ,使 ,连接 、 、 .若 ,则 ( ) A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
9. 方程 的解是 .10. 把方程 化成一般形式 .11. 一个口袋中有3个红球、7个白球,这些球除颜色外都相同,从口袋中随机摸出一个球,这个球是红球的概率是 .12. 若关于 的一元二次方程 有一个根是1,则 .13. 如图在 中, , 的平分线 交 于点 , ,则点 到 的距离是 .
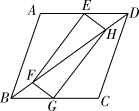
 14. 某种水果的原价为30元/箱,经过连续两次降价后的售价为15元/箱.设平均每次降价的百分率为 ,根据题意列方程是 .15. 如图,在平行四边形 ABCD 中,AB=6,AD=9,∠BAD 的平分线交BC 于点 E,交 DC 的延长线于点 F,BG⊥AE,垂足为 G,BG=4 ,则△CEF 的周长为 .
14. 某种水果的原价为30元/箱,经过连续两次降价后的售价为15元/箱.设平均每次降价的百分率为 ,根据题意列方程是 .15. 如图,在平行四边形 ABCD 中,AB=6,AD=9,∠BAD 的平分线交BC 于点 E,交 DC 的延长线于点 F,BG⊥AE,垂足为 G,BG=4 ,则△CEF 的周长为 .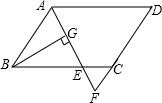 16. 已知方程 的两根为 和 ,且 ,则 .
16. 已知方程 的两根为 和 ,且 ,则 .三、解答题
-
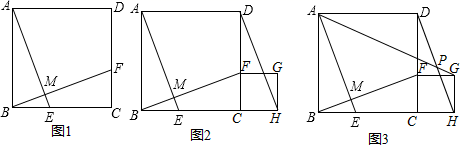
17. 解方程:(用适当的方法解方程)(1)、 .(2)、(3)、18. 新华商场为迎接家电下乡活动销售某种冰箱,每台进价为2500元,市场调研表明;当销售价定为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台,商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?19. 小明和小丽想利用摸球游戏来决定谁去参加学校举办的歌咏比赛,游戏规则是:在一个不透明的袋子里装有除数字以外其他均相同的4个小球,上面分别标有数字1、2、3、4.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和奇数,则小明去参赛;否则小丽去参赛.(1)、用树状图或列表法求出小明参赛的概率;(2)、你认为这个游戏公平吗?请说明理由.20. 如图1,在 中, ,求作菱形 ,使点 在边 上,点 、 在边 上,点 在 上.
 小明的作法:①如图2,在边 上取一点 ,过点 作 交 于点 .
小明的作法:①如图2,在边 上取一点 ,过点 作 交 于点 .②以点 为圆心, 长为半径画弧,交 于点 .
③在 上截取 ,连接 ,则四边形 为所求作的菱形.
证明:小明所作的四边形 是菱形
21. 已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.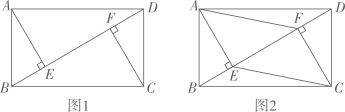 (1)、如图1,求证:AE=CF;(2)、如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的 .
(1)、如图1,求证:AE=CF;(2)、如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的 .