辽宁省阜新市新邱区2020-2021学年九年级上学期数学期中试卷
试卷更新日期:2021-09-10 类型:期中考试
一、单选题
-
1. 一元二次方程x2﹣x﹣2=0的解是( )A、x1=﹣1,x2=﹣2 B、x1=1,x2=﹣2 C、x1=1,x2=2 D、x1=﹣1,x2=22. 某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )A、(3+x)(4-0.5x)=15 B、(x+3)(4+0.5x)=15 C、(x+4)(3-0.5x)=15 D、(x+1)(4-0.5x)=153. 一元二次方程 的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根4. 一元二次方程x2﹣2x+m=0总有实数根,则m应满足的条件是( )A、m>1 B、m=1 C、m<1 D、m≤15. 一个不透明的盒子中装有2个白球,5个红球和8个黄球,这些球除颜色外,没有任何其他区别,从这个盒子中随机摸出一个球,摸到红球的概率为( )A、 B、 C、 D、6. 下列图形中,是中心对称图形但不一定是轴对称图形的是( )A、矩形 B、菱形 C、正方形 D、平行四边形7. 若菱形的边长为2cm,其中一内角为60°,则它的面积为( )A、 B、 C、 D、8. 在平行四边形ABCD中,∠B=110°,延长AD至F,延长CD至E,连接EF,则∠E+∠F=( )
 A、110° B、30° C、50° D、70°9. 如图所示,将矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕线MN上,(如图点B’),若 ,则折痕AE的长为( )
A、110° B、30° C、50° D、70°9. 如图所示,将矩形ABCD纸对折,设折痕为MN,再把B点叠在折痕线MN上,(如图点B’),若 ,则折痕AE的长为( )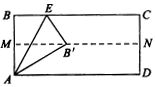 A、 B、 C、2 D、10.
A、 B、 C、2 D、10.已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
 A、6cm B、4cm C、3cm D、2cm
A、6cm B、4cm C、3cm D、2cm二、填空题
-
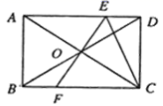
11. 方程(x-1)(2x+1)=2化成一般形式是 .12. 已知关于x的方程 有两个不相等的实数根,则m的最大整数值是 .13. 已知菱形ABCD的边长为6, ,如果点P是菱形内一点,且 ,那么 的长为.14. 如图,矩形 的两条对角线交于点 ,过点 作 的垂线 ,分别交 , 于点 , ,连接 ,已知△ 的周长为24cm,则矩形 的周长是cm.
 15. 一天上午林老师来到某中学参加该校的校园开放日活动,他打算随机听一节九年级的课程,下表是他拿到的当天上午九年级的课表,如果每一个班级的每一节课被听的可能性是一样的,那么听数学课的可能性是 .
15. 一天上午林老师来到某中学参加该校的校园开放日活动,他打算随机听一节九年级的课程,下表是他拿到的当天上午九年级的课表,如果每一个班级的每一节课被听的可能性是一样的,那么听数学课的可能性是 .班级
节次
1班
2班
3班
4班
第1节
语文
数学
外语
化学
第2节
数学
政治
物理
语文
第3节
物理
化学
体育
数学
第4节
外语
语文
政治
体育
16. 如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 .
三、解答题
-
17. 按要求的方法解方程,否则不得分.(1)、 (配方法)(2)、 (公式法)(3)、 (因式分解法)18. 某工厂生产的某种产品按质量分为10个档次,第一档次(最低档次)的产品一天能生产95件,每件利润6元,每提高一个档次,每件利润增加2元,但一天产量减少5件.(1)、若生产第x档次的产品一天的总利润为y元(其中x为正整数,且 ),求出y关于x的函数关系式;(2)、若生产第x档次的产品一天的总利润为1120元,求该产品的质量档次.19. 我市某校在推进新课改的过程中,开设的体育选修课有:A:篮球,B:足球,C:排球,D:羽毛球,E:乒乓球,学生可根据自己的爱好选修一门,学校李老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).
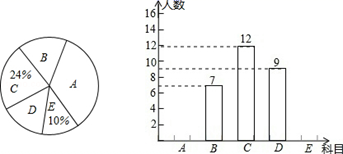 (1)、请你求出该班的总人数,并补全频数分布直方图;(2)、该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.20. 如图,在▱ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.
(1)、请你求出该班的总人数,并补全频数分布直方图;(2)、该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.20. 如图,在▱ABCD中,AE⊥BC于点E点,延长BC至F点使CF=BE,连接AF,DE,DF.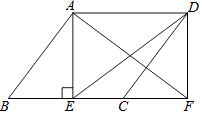 (1)、求证:四边形AEFD是矩形;(2)、若AB=6,DE=8,BF=10,求AE的长.21. 在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.(1)、
(1)、求证:四边形AEFD是矩形;(2)、若AB=6,DE=8,BF=10,求AE的长.21. 在正方形ABCD和正方形DEFG中,顶点B、D、F在同一直线上,H是BF的中点.(1)、如图1,若AB=1,DG=2,求BH的长;
 (2)、
(2)、如图2,连接AH,GH.

小宇观察图2,提出猜想:AH=GH,AH⊥GH.小宇把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:延长AH交EF于点M,连接AG,GM,要证明结论成立只需证△GAM是等腰直角三角形;
想法2:连接AC,GE分别交BF于点M,N,要证明结论成立只需证△AMH≌△HNG.
…
请你参考上面的想法,帮助小宇证明AH=GH,AH⊥GH.(一种方法即可)
22. 如图,正方形ABCD的边长是3,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转 得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF,CF. (1)、如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;(2)、如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;
(1)、如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形;(2)、如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由;