辽宁省鞍山市立山区2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-09-10 类型：期中考试

进入出卷网下载

一、单选题

1. 下列汽车标志中，可以看作是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列方程中，①2x²﹣1＝0；②ax²+bx+c＝0；③（x+2）（x﹣3）＝x²﹣3；④2x $- \frac{1}{x}$ $=$ 0．是一元二次方程的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 如图，在△ABC中，∠CAB＝65°，在同一平面内，将△ABC绕点A按逆时针方向旋转到△AB'C'的位置，使得CC′∥AB，则∠BAB′＝（）

A、30° B、35° C、40° D、50°

查看试题解析
4. 如图，点D在△ABC的边AC上，要判断△ADB与△ABC相似，添加一个条件，错误的是（）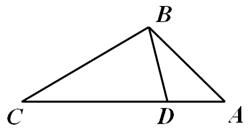

A、∠ABD=∠C B、∠ADB=∠ABC C、 $\frac{AB}{BD} = \frac{CB}{CD}$ D、 $\frac{AD}{AB} = \frac{AB}{AC}$

查看试题解析
5. 如图中的两个三角形是位似图形，点M的坐标为 $(3 ， 2)$ ，则它们位似中心的坐标是（）

A、 $(0 ， 2)$ B、 $(0 ， 3)$ C、 $(2 ， - 1)$ D、 $(2 ， 3)$

查看试题解析
6. 飞机着陆后滑行的距离y（单位：m）关于滑行时间t（单位：s）的函数解析式是y＝60t﹣ $\frac{6}{5}$ t² ，飞机着陆至停下来共滑行（）

A、25米 B、50米 C、625米 D、750米

查看试题解析
7. 若关于x的一元二次方程x²﹣3x+p=0（p≠0）的两个不相等的实数根分别为a和b，且a²﹣ab+b²=18，则 $\frac{a}{b}$ + $\frac{b}{a}$ 的值是（）

A、3 B、﹣3 C、5 D、﹣5

查看试题解析
8. 已知二次函数y=ax²+bx+c的图象如图所示．下列结论：①abc＞0；②2a﹣b＜0；③4a﹣2b+c＜0；④（a+c）²＜b²其中正确的个数有（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 一元二次方程y²﹣y $- \frac{3}{4} =$ 0配方后可化为．

查看试题解析
10. 如图，△ABC中，∠BAC＝40°，把△ABC绕点A逆时针旋转60°，得△ADE，则∠EAC的度数为．

查看试题解析
11. 如图，在宽为18米、长为24米的矩形地面上修筑同样宽的道路（图中阴影部分），余下部分种植草坪，要使草坪的面积为整个矩形面积的 $\frac{3}{4}$ ，设道路的宽为x米，则可列方程为．

查看试题解析
12.
如图，在平面直角坐标系中，点A、B的坐标分别为（3，2）、（﹣1，0），若将线段BA绕点B顺时针旋转90°得到线段BA′，则点A′的坐标为．

查看试题解析
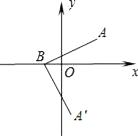13. 当 $- 2 \leq x \leq 1$ 时，二次函数 $y = - {(x - m)}^{2} + m^{2} + 1$ 有最大值4，则实数m的值为．

查看试题解析
14. 如图，以矩形ABOD的两边OD、OB所在直线为坐标轴建立直角坐标系．若E是AD的中点，将△ABE沿BE折叠后得到△GBE，延长BG交OD于F点，若OF＝1，FD＝2，则G点的坐标为．

查看试题解析
15. 已知抛物线y＝x²﹣（4m+1）x+2m﹣1与x轴交于两点，如果有一个交点的横坐标大于2，另一个交点的横坐标小于2，并且抛物线与y轴的交点在点（0， $- \frac{1}{2}$ ）的下方，那么m的取值范围是．

查看试题解析
16. 在平面直角坐标系中，正方形ABCD的位置如图所示，点A的坐标为 $(1 ， 0)$ ，点D的坐标为 $(0 ， 2)$ ，延长CB交x轴于点 $A_{1}$ ，作正方形 $A_{1} B_{1} C_{1} C$ ，延长 $C_{1} B_{1}$ 交x轴于点 $A_{2}$ ，作正方形 $A_{2} B_{2} C_{2} C_{1} \dots$ 按这样的规律进行下去，第2020个正方形的面积为．

查看试题解析

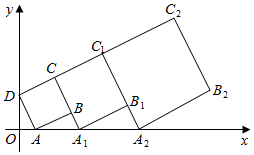
三、解答题

17.

(1)、x²﹣3x+2＝0；

(2)、3x²+5（2x+1）＝0（公式法）．

查看试题解析
18. 每个小方格都是边长为1个单位长度，正方形ABCD在坐标系中的位置如图所示．

(1)、画出正方形ABCD关于原点中心对称的图形；

(2)、画出正方形ABCD绕点D点顺时针方向旋转90°后的图形；

(3)、求出正方形ABCD的点B绕点D点顺时针方向旋转90°后经过的路线长．

查看试题解析
19. 已知关于x的方程x²﹣（4﹣2m）x+3﹣6m＝0．

(1)、求证：无论m取何值时，方程总有实数根；

(2)、是否存在非负整数m，使方程的两个根均为正数？若存在，请求出m的值，并求出此时方程的两个根；若不存在，请说明理由．

查看试题解析
20. 如图，学校为了照明，在墙BC上方安装一个小型灯杆AB（点A为灯泡的位置，A、B、C三点在一直线上），当小明站在E处时，他在地面上的影长EF＝1m，小亮站在H处时，他在地面上的影长HM＝1.6m．小亮和小明之间的距离HE＝4m，已知小明的身高DE为1.5m．小亮的身高CH为1.6m，灯杆AB的高为1.8m，求墙BC的高．

查看试题解析
21. 在疫情影响下，口罩的需求量猛增，某口罩厂从2020年1月口罩生产数量2万个增长到2020年3月口罩生产数量2.88万个．

(1)、求该口罩厂这两个月生产数量的月平均增长率？

(2)、按照这样的月平均增长速度，4月份的口罩生产数量能达到多少万个？

查看试题解析
22. 如图（1），平行四边形ABCD中，∠B＝45°，连接AC，AC＝AB＝5cm；△ABC不动，将△ACD绕点A顺时针旋转α度（0°＜α＜135°），旋转后点C的对应点为点E，点D的对应点为点F，AF、AE（或它们的延长线）交直线BC于点H、G，如图（2）．

(1)、如图（2），找出图中与△AGC相似的三角形（不添加字母），并证明；

(2)、在旋转过程中，当△AGH是等腰三角形时，求CG的长．

查看试题解析
23. 某公司的商品进价每件60元，售价每件130元，为了支持“抗新冠肺炎”，每销售一件捐款4元．且未来30天，该商品将开展每天降价1元”的促销活动，即从第一天起每天的单价均比前一天降1元，市场调查发现，设第x天（1≤x≤30且x为整数）的销量为y件，y与x满足一次函数数关系，其对应数据如表：

X（天）

……

1

3

5

7

……

Y（件）

……

35

45

55

65

……

(1)、直接写出y与x的函数关系式；

(2)、在这30天内，哪一天去掉捐款后的利润是6235元？

(3)、设第x天去掉捐款后的利润为W元，试求出W与x之间的函数关系式，并求出哪一天的利润最大，最大利润是多少元？

查看试题解析
24. 已知：∠AOB＝∠COD＝90°，OA＝OB，OC＝OD．（OC $> \fr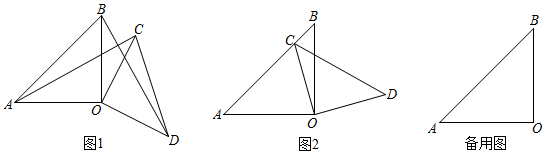ac{\sqrt{2}}{2}$ OA）

(1)、如图1：连AC、BD，判断：AC与BD之间的关系；并说明理由．

(2)、若将△COD绕点O逆时针旋转，
①如图2，当点C恰好在AB边上时，请写出AC、BC、OC之间数量关系；并说明理由．

②当点B、D、C在同一条直线上时，若OB＝6，OC＝5，求AC的长．

查看试题解析
25. 如图，抛物线y＝ax²+bx+2（a≠0）与x轴交于A（﹣1，0）、B（4，0）两点，与y轴交于点C．

(1)、求抛物线的解析式；

(2)、当点P是直线BC下方的抛物线上一点，且S_△PBC＝2S_△ABC时，求点P的坐标；

(3)、点P（﹣2，﹣3），点E是抛物线上一点，点F是抛物线对称轴上一点，是否存在这样的点E和点F，使得以点B、P、E、F为顶点的四边形是平行四边形？若存在，请直接写出点F的坐标；若不存在，请说明理由．

查看试题解析

X（天）	……	1	3	5	7	……
Y（件）	……	35	45	55	65	……