安徽省滁州市定远县2020-2021学年九年级上学期数学期中试卷

试卷更新日期：2021-09-10 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $\frac{y}{x}$ = $\frac{3}{4}$ ，则 $\frac{x + y}{x}$ 的值为（　　）

A、1 B、 $\frac{4}{7}$ C、 $\frac{5}{4}$ D、 $\frac{7}{4}$

查看试题解析
2. 下列函数中，反比例函数是（）

A、x（y+1）＝1 B、 $y = \frac{1}{x + 1}$ C、 $y = \frac{1}{x^{2}}$ D、 $y = \frac{1}{3 x}$

查看试题解析
3. 若函数y=4x²+1的函数值为5，则自变量x的值应为（　　）

A、1 B、-1 C、±1 D、 $\frac{3 \sqrt{2}}{2}$

查看试题解析
4. 在同一坐标系中，抛物线y＝4x² ， y＝ $\frac{1}{4}$ x² ， y＝－ $\frac{1}{4}$ x²的共同特点是（）

A、关于y轴对称，开口向上 B、关于y轴对称，y随x的增大而增大 C、关于y轴对称，y随x的增大而减小 D、关于y轴对称，顶点是原点

查看试题解析
5. 已知二次函数y=a（x﹣h）²+k（a＞0），其图象过点A（0，2），B（8，3），则h的值可以是（　　）

A、6 B、5 C、4 D、3

查看试题解析
6. 下列各问题中，两个变量之间的关系不是反比例函数的是（）

A、小明完成100m赛跑时，时间t（s）与跑步的平均速度v（m/s）之间的关系. B、菱形的面积为48cm² ，它的两条对角线的长为y（cm）与x（cm）的关系. C、一个玻璃容器的体积为30L时，所盛液体的质量m与所盛液体的体积V之间的关系. D、压力为600N时，压强p与受力面积S之间的关系.

查看试题解析
7. 如图，AB、CD相交于点O，AD∥CB，若AO=2，BO=3，CD=6，则CO等于（）

A、2.4 B、3 C、3.6 D、4

查看试题解析
8.
如图，平面直角坐标系中，点M是直线y=2与x轴之间的一个动点，且点M是抛物线y= $\frac{1}{2}$ x²+bx+c的顶点，则方程 $\frac{1}{2}$ x²+bx+c=1的解的个数是（　　）

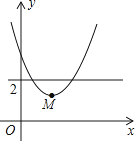A、0或2 B、0或1 C、1或2 D、0，1或2

查看试题解析
9. 如图，已知点C是线段AB的黄金分割点（其中AC＞BC），则下列结论正确的是（）

A、 $\frac{B C}{A C} = \frac{\sqrt{5} - 1}{2}$ B、 $\frac{A C}{B C} = \frac{\sqrt{5} - 1}{2}$ C、AB²＝AC²+BC² D、BC²＝AC•BA

查看试题解析
10.
如图，已知四边形OABC是菱形，CD⊥x轴，垂足为D，函数y= $\frac{4}{x}$ 的图象经过点C，且与AB交于点E．若OD=2，则△OCE的面积为（　　）

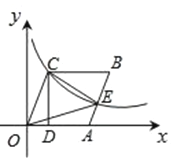A、2 B、4 C、2 $\sqrt{2}$ D、4 $\sqrt{2}$

查看试题解析

二、填空题

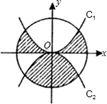
11. 在比例尺为1：5000的地图上，量得甲、乙两地的距离为25cm，则甲、乙两地间的实际距离是km.

查看试题解析
12. 如图，圆O的半径为2.C₁是函数y=x²的图象，C₂是函数y=−x²的图象，则阴影部分的面积是.

查看试题解析
13. 已知实数x，y，z满足x+y+z＝0，3x﹣y﹣2z＝0，则x：y：z＝．

查看试题解析
14. 如图，在正方形ABCD中， $△$ BPC是等边三角形，BP，CP的延长线分别交AD于点E，F，连接BD，DP，BD与CF相交于点H．给出以下结论：①AF＝DE；②∠ADP＝15°；③ $\frac{P F}{P C} = \frac{1}{3}$ ；④PD²＝PH•PB，其中正确的是．（填写正确结论的序号）

查看试题解析

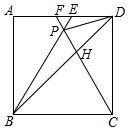
三、解答题

15. 已知a、b、c为三角形ABC的三边长，且 $a + b + c = 36$ ， $\frac{a}{3} = \frac{b}{4} = \frac{c}{5}$ ，求三角形ABC三边的长．

查看试题解析
16. 已知二次函数的顶点坐标为（1，4），且其图象经过点（﹣2，﹣5），求此二次函数的解析式．

查看试题解析
17. 新冠疫情暴发后，口罩的需求量增大．某口罩加工厂承揽生产1600万个口罩的任务，计划用t天完成．

(1)、写出每天生产口罩w（万个）与生产时间t（天）（t＞4）之间的函数表达式；

(2)、由于国外的疫情形势严峻，卫生管理部门要求厂家提前4天交货，那么加工厂每天要多做多少万个口罩才能完成任务？（用含t的代数式表示）

查看试题解析
18. 如图，D、E分别是 $△$ ABC的边AB、BC上的点，DE∥AC，若 $S_{△ B D E} ： S_{△ C D E}$ ＝1：3，求 $S_{△ D O E} ： S_{△ A O C}$ 的值．

查看试题解析
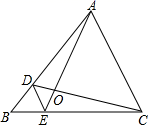19. 抛物线y＝mx²﹣4m（m＞0）与x轴交于A，B两点（A点在B点左边），与y轴交于C点，已知OC＝2OA．求：

(1)、A，B两点的坐标；

(2)、抛物线的解析式．

查看试题解析
20. 如图，点P是菱形ABCD的对角线AC上一点，连接DP并延长，交AB于点F，交CB的延长线于点E．求证：

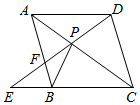(1)、 $△$ APB≌ $△$ APD；

(2)、PD²＝PE•PF．

查看试题解析
21. 如图，在平面直角坐标系中有抛物线c：y＝x²+m和直线l：y＝﹣2x﹣2，直线l与x轴的交点为B，与y轴的交点为A．

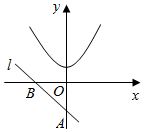(1)、求m取何值时，抛物线c与直线l没有公共点；

(2)、向下平移抛物线c，当抛物线c的顶点与点A重合时，试判断点B是否在平移后的抛物线上．

查看试题解析
22. 反比例函数y＝ $\frac{k}{x}$ （k≠0，x＞0）的图象与直线y＝3x相交于点C，过直线上点A（1，3）作AB⊥x轴于点B，交反比例函数图象于点D，且AB＝3BD.

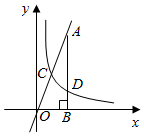(1)、求k的值；

(2)、在y轴上确定一点M，使点M到A，B两点距离之和d＝MA+MB最小，求点M的坐标.

查看试题解析
23. 在 $△$ ABC中，∠C＝90°，AC＝BC，点M，N分别在AC，BC上，将 $△$ ABC沿MN折叠，顶点C恰好落在斜边的P点上．

(1)、如图1，若点N为BC中点时，求证：MN∥AB；

(2)、如图2，当MN与AB不平行时，求证： $\frac{P A}{P B} = \frac{C M}{C N}$ ；

(3)、如图3，当AC≠BC且MN与AB不平行时，（2）中的等式还成立吗？请直接写出结论．

查看试题解析