广东省揭阳市普宁市2020-2021学年高一上学期数学期中考试试卷
试卷更新日期:2021-09-09 类型:期中考试
一、单选题
-
1. 若集合 , ,则 等于( )A、 B、 C、 D、2. 命题“ ”的否定是( )A、 B、 C、 D、3. 设 是定义在 上的偶函数,当 时, ,则 ( )A、-1 B、-3 C、1 D、34. 设 , 则 “ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件5. 若命题“ ”是真命题,则实数 的取值范围是( )A、 B、 C、 D、6. 下列函数中,既是奇函数又是增函数的为A、 B、 C、 D、7. 小明骑车上学,开始时匀速行驶,途中因交通堵塞停留了一段时间,后为了赶时间加快速度行驶.与以上事件吻合得最好的图象是( )A、
 B、
B、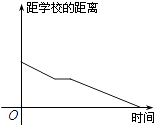 C、
C、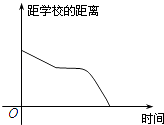 D、
D、 8. 当函数 ,取得最小值时, ( )A、 B、 C、 D、
8. 当函数 ,取得最小值时, ( )A、 B、 C、 D、二、多选题
-
9. 已知集合 有下列四个式子,其中正确的是( )A、 B、 C、 D、10. 下列函数中,满足 的是( )A、 B、 C、 D、11. 已知幂函数 ,下列说法正确的有( )A、 B、如果 是偶函数,则 一定是偶数 C、 的图像恒经过定点 和 D、 的图像与x轴正半轴没有交点12. 已知 ,不等式 的解集是 ,下列说法正确的是( )A、 B、 C、关于 的不等式 的解集是 D、如果 ,则
三、填空题
-
13. 某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为14. 函数y= 的定义域是.15. 已知 , ,则 的取值范围是.16. 设函数 ,则 :如果 ,则 .
四、解答题
-
17. 设 为定义在R上的偶函数,当 时, ;当 时, ,直线 与抛物线 的一个交点为 ,如图所示.
 (1)、当 时,写出 的递增区间(不需要证明);(2)、补全 的图像,并根据图像写出不等式 的解集,18. 已知集合 ,若 ,求实数m的值.19.(1)、已知 ,求 的最大值(2)、已知 , 均为正实数,若 ,求 的最大值20. 已知函数 为 上的奇函数,且 .(1)、求 ;(2)、判断 在 上的单调性并证明.21. 已知 ,奇函数 与偶函数 的定义域均为 ,且满足 .(1)、分别求 和 的解析式:(2)、若对任意 恒成立,试求实数a的取值范围.22. 经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2018年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足 (其中 ,a为正常数).已知生产该产品还需投入成本 万元(不含促销费用),每一件产品的销售价格定为 元,假定厂家的生产能力完全能满足市场的销售需求.(1)、将该产品的利润y万元表示为促销费用x万元的函数;(2)、促销费用投入多少万元时,厂家的利润最大?并求出最大利润的值.
(1)、当 时,写出 的递增区间(不需要证明);(2)、补全 的图像,并根据图像写出不等式 的解集,18. 已知集合 ,若 ,求实数m的值.19.(1)、已知 ,求 的最大值(2)、已知 , 均为正实数,若 ,求 的最大值20. 已知函数 为 上的奇函数,且 .(1)、求 ;(2)、判断 在 上的单调性并证明.21. 已知 ,奇函数 与偶函数 的定义域均为 ,且满足 .(1)、分别求 和 的解析式:(2)、若对任意 恒成立,试求实数a的取值范围.22. 经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2018年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足 (其中 ,a为正常数).已知生产该产品还需投入成本 万元(不含促销费用),每一件产品的销售价格定为 元,假定厂家的生产能力完全能满足市场的销售需求.(1)、将该产品的利润y万元表示为促销费用x万元的函数;(2)、促销费用投入多少万元时,厂家的利润最大?并求出最大利润的值.