广东省佛山市南海区2020-2021学年高一上学期数学期中考试试卷
试卷更新日期:2021-09-09 类型:期中考试
一、单选题
-
1. 如图,已知全集 ,集合 ,则图中阴影部分表示的集合是( )
 A、 B、 C、 D、2. 已知命题p: , ,则 是( )A、 , B、 , C、 , D、 ,3. 如图中,可作为函数y=f(x)图象的是( )A、
A、 B、 C、 D、2. 已知命题p: , ,则 是( )A、 , B、 , C、 , D、 ,3. 如图中,可作为函数y=f(x)图象的是( )A、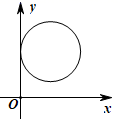 B、
B、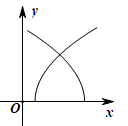 C、
C、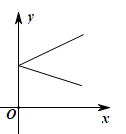 D、
D、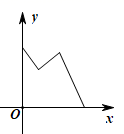 4. 设 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件5. 下列函数中是偶函数,且在 上单调递增的是( )A、 B、 C、 D、6. 函数 和 的图象关于( )A、 轴对称 B、 轴对称 C、原点对称 D、直线 对称7. 定义在 上的奇函数 满足 且对任意的正数 、 ( ),有 ,则不等式 的解集是( )A、 B、 C、 D、8. 高斯是德国著名的数学家,近代数学奠基者之一,用他的名字命名了“高斯函数”.设 ,用 表示不超过 的最大整数,则 称为高斯函数.例如: , ,已知函数 ,则下列选项中,正确的是( )A、 的最大值为1,没有最小值 B、 的最小值为0,没有最大值 C、 没有最大值,没有最小值 D、 的最大值为1,最小值为0
4. 设 ,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充要条件 D、既不充分也不必要条件5. 下列函数中是偶函数,且在 上单调递增的是( )A、 B、 C、 D、6. 函数 和 的图象关于( )A、 轴对称 B、 轴对称 C、原点对称 D、直线 对称7. 定义在 上的奇函数 满足 且对任意的正数 、 ( ),有 ,则不等式 的解集是( )A、 B、 C、 D、8. 高斯是德国著名的数学家,近代数学奠基者之一,用他的名字命名了“高斯函数”.设 ,用 表示不超过 的最大整数,则 称为高斯函数.例如: , ,已知函数 ,则下列选项中,正确的是( )A、 的最大值为1,没有最小值 B、 的最小值为0,没有最大值 C、 没有最大值,没有最小值 D、 的最大值为1,最小值为0二、多选题
-
9. 已知函数 的图象过点(3,27),下列说法正确的是( )A、函数 的图象过原点 B、函数 是奇函数 C、函数 是单调减函数 D、函数 的值域为10. 如图,某池塘里的浮萍面积 (单位: )与时间 (单位:月)的关系式为 ( ,且 ; 且 ).则下列说法正确的是( )
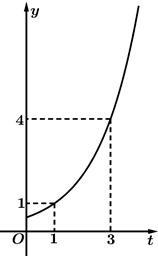 A、浮萍每月增加的面积都相等 B、第6个月时,浮萍的面积会超过 C、浮萍每月的增长率为1 D、若浮萍面积蔓延到 , , 所经过的时间分别为 , , ,则11. 已知 , , ,则( )A、 B、 C、 D、12. 对任意两个实数 , ,定义 ,若 , ,下列关于函数 的说法正确的是( )A、函数 是偶函数 B、方程 有两个实数根 C、函数 在 上单调递增,在 上单调递减 D、函数 有最大值为0,无最小值
A、浮萍每月增加的面积都相等 B、第6个月时,浮萍的面积会超过 C、浮萍每月的增长率为1 D、若浮萍面积蔓延到 , , 所经过的时间分别为 , , ,则11. 已知 , , ,则( )A、 B、 C、 D、12. 对任意两个实数 , ,定义 ,若 , ,下列关于函数 的说法正确的是( )A、函数 是偶函数 B、方程 有两个实数根 C、函数 在 上单调递增,在 上单调递减 D、函数 有最大值为0,无最小值三、填空题
-
13. 求值: .14. 若关于 的不等式 的解集为 ,则实数 的取值范围是.15. 用二分法计算 的一个正数零点附近的函数值,参考数据如下:
那么方程 的一个近似根(精确到0.1)为.
16. 中的 , 要分别满足 , 且 ,小明同学不知道为什么,请你帮他解释为.四、解答题
-
17. 设函数 的定义域为集合 ,不等式 的解集为 .(1)、求集合 , ;(2)、求集合 , ;(3)、写出集合( )与( )的关系.18. 已知 .(1)、求证: 在 上是增函数;(2)、① ,猜想 与 的大小关系;
②证明①的猜想的结论;
③求函数 的最值.
19. 若函数 . (1)、在给定的平面直角坐标系中画出函数 图象;(2)、写出函数 的值域、单调区间;(3)、在① ,② ,③ 这三个式子中任选出一个使其等于 ,求不等式 的解集.20. 人口问题是当今世界各国普遍关注的问题,认识人口数量的变化规律,可以为制定一系列政策提供依据.早在1798年,英国经济学家马尔萨斯就提出了自然状态下的人口增长模型: ,其中 表示经过的时间, 表示 时的人口数, 表示人口的年平均增长率.(1)、根据国家统计局网站公布的数据,我国1950年末、1959年末的人口总数大约分别为5.5亿和6.7亿.根据这些数据,用马尔萨斯人口增长模型建立我国在1950~1959年期间的具体人口增长模型.(精确到0.0001)(2)、以(1)中的模型作预测,大约在哪一年我国人口总数达到13亿?(参考数据: , , , , )
(1)、在给定的平面直角坐标系中画出函数 图象;(2)、写出函数 的值域、单调区间;(3)、在① ,② ,③ 这三个式子中任选出一个使其等于 ,求不等式 的解集.20. 人口问题是当今世界各国普遍关注的问题,认识人口数量的变化规律,可以为制定一系列政策提供依据.早在1798年,英国经济学家马尔萨斯就提出了自然状态下的人口增长模型: ,其中 表示经过的时间, 表示 时的人口数, 表示人口的年平均增长率.(1)、根据国家统计局网站公布的数据,我国1950年末、1959年末的人口总数大约分别为5.5亿和6.7亿.根据这些数据,用马尔萨斯人口增长模型建立我国在1950~1959年期间的具体人口增长模型.(精确到0.0001)(2)、以(1)中的模型作预测,大约在哪一年我国人口总数达到13亿?(参考数据: , , , , )
