福建省三明市三地三校2020-2021学年高一上学期数学期中联考试卷
试卷更新日期:2021-09-09 类型:期中考试
一、单选题
-
1. 不等式 的解集是( )A、 B、 或 C、 D、 或2. 函数 在 上是减函数.则( )A、 B、 C、 D、3. 计算 ( )A、 B、 C、 D、4. 已知某种细胞分裂时,由1个分裂成2个,2个分裂成4个……依此类推,那么1个这样的细胞分裂3次后,得到的细胞个数为( )A、4个 B、8个 C、16个 D、32个5. 函数 的图像大致是( )A、
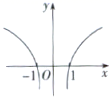 B、
B、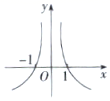 C、
C、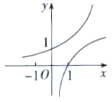 D、
D、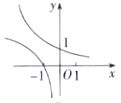 6. 函数 ( 且 )恒过定点( )A、 B、 C、 D、7. 已知 ,且 ,则 最大值为( )A、1 B、2 C、3 D、48. 若函数 在区间 上是减函数,则实数 的取值范围是( )A、 B、 C、 D、
6. 函数 ( 且 )恒过定点( )A、 B、 C、 D、7. 已知 ,且 ,则 最大值为( )A、1 B、2 C、3 D、48. 若函数 在区间 上是减函数,则实数 的取值范围是( )A、 B、 C、 D、二、多选题
-
9. 已知集合 ,则有( )A、 B、 C、 D、10. 选出下列正确的不等式( )A、 B、 C、 D、11. 下列说法正确的是( )A、命题“ ”的否定是“ ” B、命题“ ”的否定是“ ” C、“ ”是“ ”的必要而不充分条件 D、“ ”是“关于x的方程 有两个不相等的实数根”的充要条件12. 已知 ,则下列推证中不正确的是( )A、 B、 C、 D、
三、填空题
-
13. 设函数 ,则 .14. 已知函数 是定义在 上的奇函数,当 时, ,则 .15. 已知幂函数y=f(x)的图象过点(2, ),则f(9)= .16. 若函数 是奇函数,则a= .
四、解答题
-
17. 已知 , .(1)、求 、 的值;(2)、求 的值.18. 已知集合 , 或 .(1)、当 时,求 ;(2)、若 ,且“ ”是“ ”的充分不必要条件,求实数a的取值范围.19. 已知函数
 (1)、在给出的坐标系中画出函数 的图象.(2)、根据图象写出函数的单调区间和值域.20. 已知函数(1)、若函数 的图象过点 .求实数m的值,并证明函数 为奇函数;(2)、若 ,用单调性的定义证明函数 在 上单调递增.
(1)、在给出的坐标系中画出函数 的图象.(2)、根据图象写出函数的单调区间和值域.20. 已知函数(1)、若函数 的图象过点 .求实数m的值,并证明函数 为奇函数;(2)、若 ,用单调性的定义证明函数 在 上单调递增.