高中数学人教A版(2019)选择性必修一第二章 第五节直线与圆、圆与圆的位置关系同步练习
试卷更新日期:2021-09-08 类型:同步测试
一、单选题
-
1. 若直线 始终平分圆 ,则 ( )A、﹣6 B、﹣3 C、3 D、62. 圆心在C(4,-3),且与直线4x-3y=0相切的圆的方程为( )A、x2+y2+8x+6y=0 B、x2+y2+8x-6y=0 C、x2+y2-8x+6y=0 D、x2+y2-8x-6y=03. 已知圆 与圆 ,则两圆公切线条数为( )A、1 B、2 C、3 D、44. 已知直线 是圆 在点 处的切线﹐则直线 的方程为( )A、 B、 C、 D、5. 若圆 被直线3x-4y+c=0所截的弦长为 ,则c的值是( )A、6 B、-6或-16 C、-1或-21 D、16. 设直线 与圆 相交于 两点,若 ,则圆 的面积为A、 B、 C、 D、7. 若直线 被圆 所截弦长最短,则 ( )A、4 B、2 C、 D、-28. 若直线y=kx与曲线(x- )2+(|y|-1)2=1有交点,则k的取值范围是( )A、[- , ] B、[-1,1] C、[- , ] D、[- , ]
二、多选题
-
9. 直线y=kx+3被圆(x-2)2+(y-3)2=4截得的弦长为2 ,则直线的倾斜角可能为( )A、 B、 C、 D、10. 在同一直角坐标系中,直线 与圆 的位置可能是( )A、
 B、
B、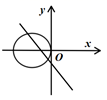 C、
C、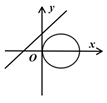 D、
D、 11. 已知圆 和圆 的交点为 , ,则( )A、圆 和圆 有两条公切线 B、直线 的方程为 C、圆 上存在两点 和 使得 D、圆 上的点到直线 的最大距离为12. 直线 分别与 轴, 轴交于 , 两点,点 在圆 上,则 面积的可能取值是( )A、 B、2 C、4 D、6
11. 已知圆 和圆 的交点为 , ,则( )A、圆 和圆 有两条公切线 B、直线 的方程为 C、圆 上存在两点 和 使得 D、圆 上的点到直线 的最大距离为12. 直线 分别与 轴, 轴交于 , 两点,点 在圆 上,则 面积的可能取值是( )A、 B、2 C、4 D、6三、填空题
-
13. 已知 为圆 : 上第二象限的一动点,直线 , 与圆 的另一个交点分别为 , ,且直线 , 的斜率之和为0,则直线 的斜率是 .14. 直线 与圆 相交于A,B两点,弦长 的最小值为 , 若 的面积为 ,则m的值为 .15. 实数 、 满足 ,则 的取值范围是 .16. 动直线 与曲线 有公共点,则 的取值范围是.
四、解答题
-
17. 已知过点 的圆M的圆心为 ,且圆M与直线 相切.(1)、求圆M的标准方程;(2)、若过点 且斜率为k的直线l交圆M于A,B两点,若 的面积为 ,求直线l的方程.18. 已知圆 经过坐标原点 ,圆心在 轴正半轴上,且与直线 相切.(1)、求圆 的标准方程.(2)、直线 : 与圆 交于 , 两点.
(i)求 的取值范围;
(ii)证明:直线 与直线 的斜率之和为定值.
19. 已知点 ,直线 及圆 .(1)、求过点M的圆C的切线方程;(2)、若直线 与圆C相切,求实数 的值;(3)、若直线 与圆C相交于A、B两点,且弦AB的长为 ,求 的值.