江苏省苏州市昆山市2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2021-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 现实生活中，如果收入1000元记作+1000元，那么－700元表示（）

A、支出700元 B、收入700元 C、支出300元 D、收入300元

查看试题解析
2. 下列各算式中，结果为负数的是（）

A、 $- (- 5)$ B、 $(- 2) \times (- \frac{2}{7})$ C、 $- | - 5 |$ D、 $2 - (- 5)$

查看试题解析
3. 去年某市户籍人口约为8790000人，其中数据8790000用科学记数法表示为（）

A、 $8.79 \times 10^{7}$ B、 $8.79 \times 10^{6}$ C、 $8.79 \times 10^{5}$ D、 $8.79 \times 10^{4}$

查看试题解析
4. 下列计算正确的是（）

A、 $3 b - 2 b = 1$ B、 $4 a^{2} + a^{3} = 5 a^{5}$ C、 $- 3 (a - 2 b) = - 3 a + 2 b$ D、 $3 a^{2} b - 5 b a^{2} = - 2 b a^{2}$

查看试题解析
5. 单项式 $- \frac{2}{3} a b^{2}$ 的系数与次数分别是m与n，则（）

A、 $m = \frac{2}{3}$ ， $n = 2$ B、 $m = - \frac{2}{3}$ ， $n = 2$ C、 $m = \frac{2}{3}$ ， $n = 3$ D、 $m = - \frac{2}{3}$ ， $n = 3$

查看试题解析
6. 一元一次方程 $2 x = 3 x - 5$ 变形正确的是（）

A、 $3 x = 2 x - 5$ B、 $3 x - 2 x = 5$ C、 $3 x - 2 x = - 5$ D、 $3 x + 2 x = 5$

查看试题解析
7. 如果单项式 $- 2 x^{2} y^{3 n}$ 与 $7 x^{m} y^{3}$ 是同类项，则 $m - n$ 的值是（）

A、3 B、2 C、1 D、 $- 1$

查看试题解析
8. 数轴上点A表示的数为-1.则与点A相距3个单位长度的点B表示的数是（）

A、 $- 4$ B、 $- 4$ 或2 C、2或 $- 2$ D、2

查看试题解析
9. 若m为有理数，则|m|－m一定是（）

A、零 B、非负数 C、正数 D、负数

查看试题解析
10. 一元一次方程 $\frac{x}{3 \times 4} + \frac{x}{4 \times 5} + \frac{x}{5 \times 6} + \frac{x}{6 \times 7} = 4$ 的解为（）

A、30 B、24 C、21 D、12

查看试题解析

二、填空题

11. $- 2 \frac{1}{5}$ 的倒数是.

查看试题解析
12. $- (- \frac{3}{5}) = \frac{8}{5}$ .

查看试题解析
13. 小明沿一条直路走了 $3 km$ 后，再以 $4 km / h$ 的速度继续往前走了 $t h$ ，那么小明共走了 $km$ .

查看试题解析
14. 比较大小： $- \frac{2}{3}$ $- \frac{5}{7}$ (填“＜”、“＝”或“＞”）.

查看试题解析
15. 有理数a、b在数轴上的位置如图所示，则 $| a - b | =$ ．

查看试题解析
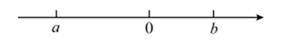16. “！”是基斯顿·卡曼于1808年发明的一种数学运算符号，叫做阶乘.自然数 $n$ 的阶乘写作 $n!$ ，并且知道： $1! = 1$ ， $2! = 2 \times 1 = 2$ ， $3! = 3 \times 2 \times 1 = 6$ ，……那么 $\frac{20!}{21!}$ 等于.

查看试题解析
17. 若方程 $(m + 2) x^{| m | - 1} + 2 = m$ 是关于x的一元一次方程，则m的值为.

查看试题解析
18. 小静同学按如图所示的程序输入一个正整数x，最后输出的结果为2031，则满足条件的x的不同值最多有个.

查看试题解析

三、解答题

19. 计算

(1)、 $(- 2) - (- 3.6) + (- 1) - 3.6$

(2)、 $(- 49) \div \frac{7}{5} \times \frac{5}{7} \div (- 25)$

(3)、 ${(- 1)}^{2020} - [1 + 3 \times (- 4)] \div (- 2^{2})$

查看试题解析
20.

(1)、 $2 a + 5 b - 3 a - b + 1$

(2)、 $5 (3 a^{2} b - a b^{2}) - 4 (- 2 a b^{2} + \frac{1}{2} a^{2} b)$

查看试题解析
21.

(1)、 $2 (3 x + 4) = 3 + 5 (x + 1)$

(2)、 $\frac{x - 1}{2} - 2 = \frac{2 - 3 x}{4}$

查看试题解析
22. 先化简，再求值： $\frac{3}{2} x - (- \frac{1}{2} x - \frac{2}{3} y^{2}) - (3 x + \frac{1}{3} y^{2})$ ，其中 $x = - 1$ ， $y = 3$ .

查看试题解析
23. 已知 $x = - 2$ 是关于x的方程 $a (x + 3) = \frac{1}{2} a + x$ 的解，求代数式 $a^{2} - 2 a + 1$ 的值.

查看试题解析
24. 已知 $A - B = 7 a^{2} - 7 a b$ ，其中 $B = - 4 a^{2} + 6 a b + 7$ ，且 $| a + 1 | + {(b - 2)}^{2} = 0$ .

(1)、填空： $a =$ ， $b =$ ；

(2)、求A的值.

查看试题解析
25. 有一段总长为a米的篱笆，利用它和一面墙（墙足够长）围成如图所示长方形菜园，其中与墙平行的篱笆处留一个长为1米的门，方便人员进出菜园.

(1)、用含有a，x的代数式表示菜园的面积；

(2)、当 $a = 50$ 米， $x = 10$ 米时，求菜园的面积.

查看试题解析
26. 现定义某种运算“ $\otimes$ ”，观察下列各式：
$1 \otimes 3 = 1 \times 4 + 3 = 7$ ； $3 \otimes (- 1) = 3 \times 4 - 1 = 11$ ； $5 \otimes 4 = 5 \times 4 + 4 = 24$ ； $4 \otimes (- 3) = 4 \times 4 - 3 = 13$ .

(1)、请用含a，b字母的代数式写出： $a \otimes b =$ ；

(2)、若 $a \otimes (- 2 b) = 4$ ，请计算 $(a - b) \otimes (2 a + b) - 2$ 的值：

(3)、若 $b \otimes (2 \otimes b) - 1 = 3 b$ ，求b的值.

查看试题解析
27. 已知点A是数轴上运动的点，其对应的数记为x，点B在点A的右侧，与A相距2个单位长度.

(1)、点B表示的数为；（用字母x代数式表示）

(2)、若点A在原点左侧，则点A到原点的距离为；（用字母x代数式表示）

(3)、若A、B两点间的距离等于点B到原点距离的3倍，试求字母x的值.

查看试题解析
28. （感悟数学方法）
已知： $A = 2 a b - a$ ， $B = - a b + 2 a + b$ .

(1)、计算： $5 A - 2 B$ ；

(2)、若 $5 A - 2 B$ 的值与字母b的取值无关，求a的值.

(3)、（解决实际问题）请利用上述问题中的数学方法解决下面问题：

新冠疫情期间，某医药器材经销商计划同时购进一批甲、乙两种型号的口罩.已知甲型号口罩每箱进价为800元，乙型号口罩每箱进价为600元.该医药公司根据疫情，决定购进两种口罩共20箱，有多种购进方案，现销售一箱甲型口罩，利润率为45%，乙型口罩的售价为每箱1000元.而且为了及时控制疫情，公司决定每售出一箱乙型口罩，返还顾客现金m元，甲型口罩售价不变，要使不同方案所购进的口罩全部售出后经销商最终获利相同，求m的值.

查看试题解析