四川省乐山市犍为县2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中，一定是二次根式的是（）

A、 $\sqrt{a}$ B、 $\sqrt{- 10}$ C、 $\sqrt{a + 1}$ D、 $\sqrt{a^{2} + 1}$

查看试题解析
2. 下列计算中正确的是（）

A、 $\sqrt{{(- 3)}^{2}} = - 3$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $\sqrt{27} \div \sqrt{3} = 9$ D、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$

查看试题解析
3. 如果 $x^{2} - 8 x + m = 0$ 可以通过配方写成 ${(x - n)}^{2} = 6$ 的形式，那么 $x^{2} + 8 x + m = 0$ 可以配方成（）

A、 ${(x - n + 5)}^{2} = 1$ B、 ${(x + n)}^{2} = 6$ C、 ${(x - n + 5)}^{2} = 11$ D、 ${(x + n)}^{2} = 1$

查看试题解析
4. 下列解方程的过程，正确的是（）

A、 $x^{2} = x$ ．两边同除以x，得 $x = 1$ B、 $x^{2} + 4 = 0$ ．直接开平方法，得 $x = \pm 2$ C、 $(x - 2) (x + 1) = 3 \times 2$ ．∵ $x - 2 = 3$ ， $x + 1 = 2$ ， ∴ $x_{1} = 5$ ， $x_{2} = 1$ D、 $(2 - 3 x) + {(2 - 3 x)}^{2} = 0$ ，整理得 $(2 - 3 x) (1 + 2 - 3 x) = 0$ ， ∴ $x_{1} = \frac{2}{3}$ ， $x_{2} = 1$

查看试题解析
5. 如图，点P（8，6）在△ABC的边AC上，以原点O为位似中心，在第一象限内将△ABC缩小到原来的 $\frac{1}{2}$ ，得到△A′B′C′，点P在A′C′上的对应点P′的的坐标为（）

A、（4，3） B、（3，4） C、（5，3） D、（4，4）

查看试题解析
6. 下列四条线段a、b、c、d不是成比例线段的是（）

A、 $a = 4$ ， $b = 8$ ， $c = 5$ ， $d = 10$ B、 $a = 1.1$ ， $b = 2.2$ ， $c = 3.3$ ， $d = 4.4$ C、 $a = 2$ ， $b = 2 \sqrt{15}$ ， $c = \sqrt{5}$ ， $d = 5 \sqrt{3}$ D、 $a = 0.8$ ， $b = 3$ ， $c = 0.64$ ， $d = 2.4$

查看试题解析
7. 电影《我和我的祖国》讲述了普通人与国家之间息息相关的动人故事.一上映就获得全国人民的追捧，第一天票房约3亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达10亿元，若把平均每天票房的增长率记作x，则可以列方程为（）

A、 $3 (1 + x) = 10$ B、 $3 {(1 + x)}^{2} = 10$ C、 $3 + 3 {(1 + x)}^{2} = 10$ D、 $3 + 3 (1 + x) + 3 {(1 + x)}^{2} = 10$

查看试题解析
8. “今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为（）

A、 $62.5$ 尺 B、 $57.5$ 尺 C、 $21$ 尺 D、 $16$ 尺

查看试题解析
9. 将关于x的一元二次方程 $x^{2} - p x + q = 0$ 变形为 $x^{2} = p x - q$ ，就可以将 $x^{2}$ 表示为关于x的一次多项式，从而达到“降次”的目的，又如 $x^{3} = x \cdot x^{2} = x (p x - q) =$ …，我们将这种方法称为“降次法”，通过这种方法可以化简次数较高的代数式.根据“降次法”，已知： $x^{2} - x - 1 = 0$ ，且 $x > 0$ ，则 $x^{4} - 2 x^{3} + 3 x$ 的值为（）

A、 $1 - \sqrt{5}$ B、 $3 - \sqrt{5}$ C、 $1 + \sqrt{5}$ D、 $3 + \sqrt{5}$

查看试题解析
10. 如图， $Δ A B C$ ∽ $Δ A D E$ ， $∠ B A C = ∠ D A E = 90^{°}$ ， $A B = 4$ ， $A C = 3$ ，F是 $D E$ 的中点，若点E是直线 $B C$ 上的动点，连接 $B F$ ，则 $B F$ 的最小值是（）　

A、 $\frac{5}{2}$ B、 $2$ C、 $\frac{6}{5}$ D、 $4$

查看试题解析

二、填空题

11. 在 $\sqrt{12}$ ， $\sqrt{18}$ ， $\sqrt{20}$ ， $\sqrt{\frac{2}{3}}$ 中，与 $\sqrt{2}$ 是同类二次根式的是．

查看试题解析
12. 将一元二次方程 $(3 x - 2) (x + 1) = 8 x - 3$ 化成一般形式是．

查看试题解析
13. 如图， $l_{1} ∥ l_{2} ∥ l_{3}$ ，若 $\frac{A B}{B C} = \frac{3}{2}$ ， $D F = 10$ ，则 $D E =$ ．

查看试题解析
14. 已知方程 $x^{2} + 2 x - 3 = 0$ 的解是 $x_{1} = 1$ ， $x_{2} = - 3$ ，则方程 ${(x + 3)}^{2} + 2 (x + 3) - 3 = 0$ 的解是．

查看试题解析
15. 如图1，在 $R t Δ A B C$ 中， $∠ A C B = 90^{°}$ ，点P以每秒 $1 c m$ 的速度从点A出发，沿折线 $A C \to C B$ 运动，到点B停止．过点P作 $P D ⊥ A B$ 于点D， $P D$ 的长 $y (c m)$ 与点P的运动时间x（秒）的函数图象如图2所示．当点P运动 $4$ 秒时， $P D$ 的长是．

查看试题解析
16. 如图所示，在 $Δ A B C$ 中， $B C = 4$ ，E，F分别是 $A B$ ， $A C$ 的中点．（1）线段 $E F$ 的长为；（2）若动点P在直线 $E F$ 上， $∠ C B P$ 的平分线交 $C E$ 于点Q，当点Q把线段 $E C$ 分成的两线段之比是 $1$ ∶ $2$ 时，线段 $E P$ 、 $B P$ 之间的数量关系满足 $E P + B P$ ＝．

查看试题解析

三、解答题

17. 解方程： $4 x^{2} - {(x - 1)}^{2} = 0$ ．

查看试题解析
18. 计算： $\sqrt{48} \div \sqrt{3} - \sqrt{\frac{1}{2}} \times \sqrt{12} + \sqrt{24}$ ．

查看试题解析
19. 如图，在 $Δ A B C$ 中，点D、E、F分别在 $A B$ 、 $A C$ 、 $B C$ 上， $D E$ // $B C$ ， $E F$ // $A B$ ．

(1)、求证： $Δ A D E$ ∽ $Δ E F C$ ；

(2)、如果 $A B = 6$ ， $A D = 4$ ，求 $\frac{S_{Δ A D E}}{S_{Δ E F C}}$ 的值．

查看试题解析
20. 如果关于x的一元二次方程ax²+bx+c＝0（a≠0）有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”．

(1)、请问一元二次方程x²﹣6x+8＝0是倍根方程吗？如果是，请说明理由．

(2)、若一元二次方程x²+bx+c＝0是倍根方程，且方程有一个根为2，求b、c的值．

查看试题解析
21. 已知 $a ， b ， c$ 满足 $| a - \sqrt{12} | + \sqrt{b - 4} + {(c - 2 \sqrt{3})}^{2} = 0$

(1)、求 $a ， b ， c$ 的值；

(2)、试问以 $a ， b ， c$ 为边能否构成三角形，若能构成三角形，请判断此三角形形状并求出它的面积；若不能，请说明理由.

查看试题解析
22. 有一批图形计算器，原售价为每台800元，在甲、乙两家公司销售．甲公司用如下方法促销：买一台单价为780元，买两台每台都为760元．依此类推，即每多买一台则所买各台单价均再减20元，但最低不能低于每台440元；乙公司一律按原售价的75%促销．某单位需购买一批图形计算器：

(1)、若此单位需购买12台图形计算器，应去哪家公司购买花费较少？

(2)、若此单位恰好花费7280元，在同一家公司购买了一定数量的图形计算器，请问是在哪家公司购买的，数量是多少？

查看试题解析
23. 如图，△ABC和△BEC均为等腰直角三角形，且∠ACB=∠BEC=90°，点P为线段BE延长线上一点，连接CP，以CP为直角边向下作等腰直角△CPD，线段BE与CD相交于点F．

(1)、求证： $\frac{P C}{C D} = \frac{C E}{C B}$ ；

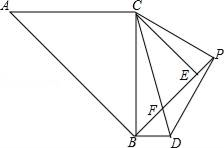(2)、连接BD，请你判断AC与BD有什么位置关系？并说明理由．

查看试题解析
24. 已知x₁、x₂是一元二次方程4kx²-4kx+k+1=0的两个实数根．

(1)、求k的取值范围．

(2)、是否存在实数k，使(2x₁-x₂)(x₁-2x₂)=- $\frac{3}{2}$ 成立？若存在求出k的值；若不存在，请说明理由．

查看试题解析
25. 如图，直线 $A B$ 分别交y轴、x轴于点A、B，其中 $O A$ 、 $O B$ 的长是方程 $x^{2} - 9 x + 18 = 0$ 的两根（ $O A > O B$ ），将直线 $A B$ 绕点O逆时针旋转 $90^{°}$ 后与x轴、y轴分别交于点C、D，点P是该直线 $C D$ 与双曲线在第一象限内的一个交点， $P E$ ⊥x轴于E，且 $S_{Δ P C E} = 16$ ．

(1)、直线 $C D$ 的解析式；

(2)、求点P的坐标；

(3)、设点Q与点P在同一个反比例函数的图象上，且点Q在直线 $P E$ 的右侧，作 $O F$ ⊥x轴于点F，当 $△ E Q F$ 与 $△ C D O$ 相似时，求点Q的横坐标．

查看试题解析
26. 如图(1)，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上的一点，连接BO交AD于点F，OE⊥OB交BC边于点E．

(1)、试说明：△ABF∽△COE．

(2)、如图(2)，当O为AC边的中点，且 $\frac{A C}{A B} = 2$ 时，求 $\frac{O F}{O E}$ 的值．

(3)、当O为AC边的中点， $\frac{A C}{A B} = n$ 时，请直接写出 $\frac{O F}{O E}$ 的值．

查看试题解析