四川省成都市大邑县2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 方程 $x^{2}$ =9的根是（）

A、x=3 B、x=-3 C、 $x_{1}$ =3， $x_{2}$ =-3 D、 $x_{1}$ = $x_{2}$ =3

查看试题解析
2. 下列四组线段中，不是成比例线段的是（）

A、a=3，b=6，c=2，d=4 B、a=1，b= $\sqrt{2}$ ，c= $\sqrt{6}$ ，d=2 $\sqrt{3}$ C、a=4，b=6，c=5，d=10 D、a=2，b= $\sqrt{5}$ ，c=2 $\sqrt{3}$ ，d= $\sqrt{15}$

查看试题解析
3. 用配方法解方程 $x^{2} - 4 x - 7 = 0$ 时，原方程应变形为（）

A、 ${(x - 2)}^{2} = 11$ B、 ${(x + 2)}^{2} = 11$ C、 ${(x - 4)}^{2} = 23$ D、 ${(x + 4)}^{2} = 23$

查看试题解析
4. 下列说法中，错误的是（　　）

A、一组对边平行且相等的四边形是平行四边形 B、两条对角线互相垂直且平分的四边形是菱形 C、四个角都相等的四边形是矩形 D、邻边相等的菱形是正方形

查看试题解析
5. 做抛掷同一枚啤酒瓶盖的重复试验，经过统计得“凸面朝上”的频率约为0.44，则可以估计抛掷这枚啤酒瓶盖出现“凸面朝上”的概率约为（）

A、22% B、44% C、50% D、56%

查看试题解析
6. 如果两个相似多边形的面积比为4：9，那么它们的周长比为（）

A、 $\sqrt{2}$ ： $\sqrt{3}$ B、2：3 C、4：9 D、16：81

查看试题解析
7. 已知点C是线段AB的黄金分割点，AC＞BC，线段AB的长为4，则线段AC的长是（）

A、2 $\sqrt{5}$ －2 B、6－2 $\sqrt{5}$ C、 $\sqrt{5}$ －1 D、3－ $\sqrt{5}$

查看试题解析
8. 如图，在 $△$ ABC中，DE∥BC，AD＝5，AB＝12，AE＝3，则AC的长是（）

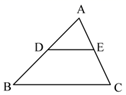A、 $\frac{36}{5}$ B、 $\frac{21}{5}$ C、20 D、15

查看试题解析
9. 如图，在菱形ABCD中，E为边CD上一点，连结AE并延长，交BC的延长线于点F，若CE＝1，DE＝2，则CF长为（　　）

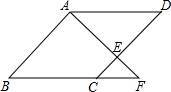A、1 B、1.5 C、2 D、2.5

查看试题解析
10. 如图，正方形ABCD的边长为4，点E在对角线BD上，且 $∠ BAE ＝ 22 . 5^{0}$ ，EF⊥AB，垂足为F，则EF的长为

A、1 B、 $\sqrt{2}$ C、 $4 - 2 \sqrt{2}$ D、 $3 \sqrt{2} - 4$

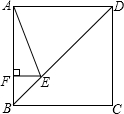查看试题解析

二、填空题

11. 已知 $\frac{b}{a} = \frac{2}{3}$ ，则 $\frac{a + b}{b}$ = ．

查看试题解析
12. 已知 $(m - 2) x^{| m |} - 3 x + 1 = 0$ 是关于x的一元二次方程，则m=.

查看试题解析
13. 如图在矩形 $A B C D$ 中，对角线 $A C ， B D$ 相交于点O，若 $∠ A C B = 30^{°} ， A B = 2$ ，则 $B D$ 的长为.

查看试题解析
14. 某同学利用标杆测旗杆的高度如图所示：标杆高度CD=2.6m，标杆与旗杆的水平距离BD=15m，人的眼睛与地面的高度EF=1.6m，人与标杆CD的水平距离DF=2m，E，C，A三点共线，则旗杆AB的高度为m.

查看试题解析
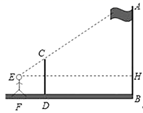15. 设m，n分别为一元二次方程 $x^{2} - 2 x - 2020 = 0$ 的两个实数根，则 $m^{2} - m + n$ ＝.

查看试题解析
16. 关于 x 的一元二次方程 $(1 - 2 k) x^{2} - 2 \sqrt{k + 1} x - 1 = 0$ 有两个不相等的实数根，则常数k的取值范围是.

查看试题解析
17. 已知a、b、c、满足 $\frac{b}{a + c} = \frac{a}{c + b} = \frac{c}{a + b} = k$ ，从下列四点：① $(1 ， \frac{1}{2})$ ；②(2，1)；③ $(1 ， - \frac{1}{2})$ ；④(1，﹣1)，中任意取一点恰好在正比例函数y＝kx图象上的概率是.

查看试题解析
18. 如图，正方形ABCD的边长AB＝4，点E、F分别是CB，DC延长线上的点，连AF交CB于点G，若BE＝1，连接AE，且∠EAF＝45°，则AG长为.

查看试题解析
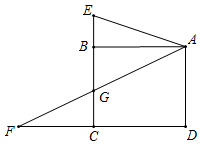19. 如图，矩形 ABCD 中，O 为 AC 中点，过点 O 的直线分别与 AB、CD 交于点 E、F，连接 BF 交 AC 于点 M，连接 DE、BO，若 $∠ C O B$ =60^o ， FO=FC，则下列结论：①FB垂直平分OC；② $△$ EOB≌ $△$ CMB ；③DE=EF；④ $S_{△ A O E} ： S_{△ B C M} = 3 ： 4$ ，⑤ $S_{△ D E F} ： S_{△ B O M} = 8 ： 3$ ，其中正确的结论是（填正确的序号）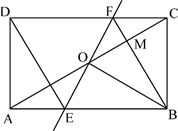

查看试题解析

三、解答题

20. 解下列方程

(1)、 $x^{2} + 2 x - 10 = 0$

(2)、 $(x - 3) (x + 4) = 18$

查看试题解析
21. 已知：关于x的方程x²+kx﹣2=0
①求证：方程有两个不相等的实数根；
②若方程的一个根是﹣1，求另一个根及k值.

查看试题解析
22. 为纪念建国70周年，某校举行班级歌咏比赛，歌曲有：《我爱你，中国》，《歌唱祖国》，《我和我的祖国》（分别用字母A，B，C依次表示这三首歌曲）．比赛时，将A，B，C这三个字母分别写在3张无差别不透明的卡片正面上，洗匀后正面向下放在桌面上，八（1）班班长先从中随机抽取一张卡片，放回后洗匀，再由八（2）班班长从中随机抽取一张卡片，进行歌咏比赛．

(1)、八（1）班抽中歌曲《我和我的祖国》的概率是；

(2)、试用画树状图或列表的方法表示所有可能的结果，并求出八（1）班和八（2）班抽中不同歌曲的概率．

查看试题解析
23. 如图，已知 $△$ ABC的三个顶点的坐标分别为A(−1，2)、B(−3，0)、C(0，0).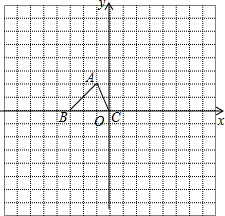

(1)、请直接写出点A关于x轴对称的点 $A^{'}$ 的坐标；

(2)、以C为位似中心，在x轴下方作 $△$ ABC的位似图形△A₁B₁C₁ ，使放大前后位似比为1：2，请画出图形，并直接写出 $△$ A₁B₁C₁的面积= ；

(3)、请直接写出：以A，B，C，D为顶点的平行四边形的第四个顶点D的坐标.

查看试题解析
24. 如图，一个农户要建一个矩形猪舍ABCD，猪舍的一边AD利用长为12米的住房墙，另外三边用25米长的建筑材料围成.为了方便进出，在CD边留一个1米宽的小门.

(1)、若矩形猪舍的面积为80平方米，求与墙平行的一边BC的长；

(2)、若与墙平行的一边BC的长度不小于与墙垂直的一边AB的长度，问BC边至少应为多少米？

查看试题解析
25. 在Rt $△$ ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F.

(1)、求证： $△$ AEF≌ $△$ DEB；

(2)、证明四边形ADCF是菱形；

(3)、若AC=6，AB=8，求菱形ADCF的面积.

查看试题解析
26. 电动自行车已成为市民日常出行的首选工具.据我市某品牌电动自行车经销商1至3月份统计，该品牌电动自行车1月份销售150辆，3月份销售216辆，且从1月份到3月份销售量的月增长率相同.

(1)、求该品牌电动自行车销售量的月增长率；

(2)、该经销商决定开拓市场，此电动自行车的进价为2000元/辆，经测算在新市场中，当售价为2750元/辆时，月销售量为200辆，若在原售价的基础上每辆降价50元，则月销售量可多售出10辆.为使月销售利润达到75000元，则该品牌电动自行车的实际售价应定为多少元？

查看试题解析
27. 如图，在菱形ABCD中，BC=10cm，BD=16cm，动点P从点B开始沿BC边匀速运动，动点Q从点D开始沿对角线DB匀速运动，它们的运动速度均为1cm/s，过点Q作QE⊥CD，与CD交于点E，连接PQ，点P和点Q同时出发，设运动时间为t（s），（0﹤t﹤10）.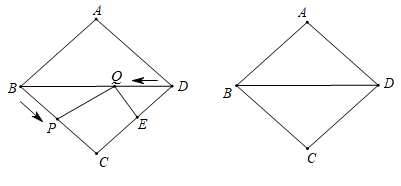

(1)、当PQ∥CD时，求t的值；

(2)、设四边形PQEC的面积为S（cm²），求S与t之间的函数关系式；

(3)、点P和点Q在运动过程中存在某一时刻t，使PQ+QE的值最小，请直接写出t的值和PQ+QE的最小值；（直接写出答案，不必说明理由）

查看试题解析
28. 矩形ABCD一条边AD=6，将矩形ABCD折叠，使得点B落在CD边上的点P处.

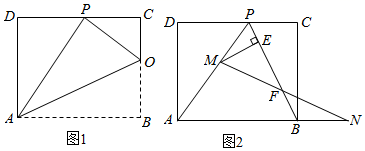(1)、如图1，已知折痕与边BC交于点O，连接AP、OP、OA.
①求证： $△$ OCP∽ $△$ PDA；

②若 $△$ OCP与 $△$ PDA的面积比为1：4，求边AB的长.

(2)、在图1中，若点P恰好是CD边的中点，求证： $2 P C^{2} = A D \cdot O B$

(3)、如图2，在（1）的条件下，擦去AO和OP，连接BP.动点M在线段AP上（不与点P、A重合），动点N在线段AB的延长线上，且BN=PM，连接MN交PB于点F，作ME⊥BP于点E. 试问动点M、N在移动的过程中，线段EF的长度是否发生变化？若不变，求出线段EF的长度；若变化，说明理由.

查看试题解析