陕西省学林大联考2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-07 类型：期中考试

进入出卷网下载

一、单选题

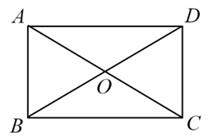
1. 方程x²﹣5＝0的实数解为（　　）

A、x₁＝ $\sqrt{5}$ ，x₂＝﹣ $\sqrt{5}$ B、x₁＝5，x₂＝﹣5 C、x＝﹣ $\sqrt{5}$ D、x＝ $\sqrt{5}$

查看试题解析
2. 若a、b、c、d是成比例线段，其中a=5cm，b=2.5cm，c=10cm，则线段d的长为（）

A、2cm B、4cm C、5cm D、6cm

查看试题解析
3. 两个相似多边形一组对应边分别为3 cm，4.5 cm，那么它们的相似比为（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、 $\frac{4}{9}$ D、 $\frac{9}{4}$

查看试题解析
4. 如图，在矩形ABCD中，AC与BD交于点O，若AB=3，AC=6，则∠AOD等于（）

A、90° B、100° C、110° D、120°

查看试题解析
5. 下列方程中，没有实数根的是（）

A、 $x^{2} - x - 2 = 0$ B、 $x^{2} - x + 1 = 0$ C、 $x^{2} - 2 x + 1 = 0$ D、 $x^{2} = 4$

查看试题解析
6. 用配方法解一元二次方程 $x^{2} + 6 x + 2 = 0$ 时，下列变形正确的是（）

A、 ${(x + 3)}^{2} = 9$ B、 ${(x + 3)}^{2} = 7$ C、 ${(x + 3)}^{2} = 3$ D、 ${(x - 3)}^{2} = 7$

查看试题解析
7. 已知 $x = 1$ 是一元二次方程 $(m - 2) x^{2} + 4 x - m^{2} = 0$ 的一个根，则m的值为（）

A、-1或2 B、-1 C、2 D、0

查看试题解析
8.
如图，已知正方形ABCD边长为1，连接AC、BD，CE平分∠ACD交BD于点E，则DE长为（）

A、2 $\sqrt{2}$ －2 B、 $\sqrt{3}$ －1 C、 $\sqrt{2}$ －1 D、2－ $\sqrt{2}$

查看试题解析
9. 某班学生毕业时都将自己的照片向全班其他学生各送一张以作留念，全班共送出1056张照片.如果全班有x名同学，根据题意，列出的方程为（）

A、 $x (x + 1) = 1056$ B、 $x (x - 1) = 1056 \times 2$ C、 $x (x - 1) = 1056$ D、 $2 x (x + 1) = 1056$

查看试题解析
10. 如图，在矩形ABCD中，点E为AD中点，BD和CE相交于点F，如果DF=2，那么线段BF的长度为（）.

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

11. 如图，已知 $△ A D E ∽ △ A B C$ ，若 $∠ A D E = 37^{\circ}$ ，则 $∠ B =$ °.

查看试题解析
12. 我市博览馆有A，B，C三个入口和D，E两个出口，小明入馆游览，他从A口进E口出的概率是.

查看试题解析
13. 如图，E、F、G、H分别是AB、BC、CD、DA的中点.要使四边形EFGH是正方形，BD、AC应满足的条件是.

查看试题解析
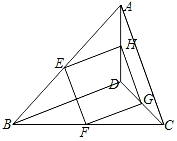14. 如图，已知菱形ABCD的边长为4，点E、F分别是AB、AD上的点，若BE＝AF＝1，∠BAD＝120°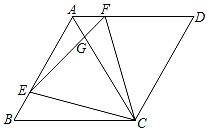， $\frac{G F}{E G}$ ＝.

查看试题解析

三、解答题

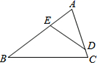
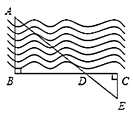
15. 解方程：（x﹣1）²＝2x+1.

查看试题解析
16. 第一个不透明的布袋中装有除颜色外均相同的7个黑球、5个白球和若干个红球每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定在0.4，估计袋中红球的个数.

查看试题解析
17. 如图，为了估算河的宽度，我们可以在河对岸选定一点A，再在河的这一边选定点B和点C，使得 $A B ⊥ B C$ ，然后选定点E，使 $E C ⊥ B C$ ，确定 $B C$ 与 $A E$ 的交点D，若测得 $B D = 180$ 米， $D C = 60$ 米， $E C = 70$ 米，请你求出小河的宽度是多少米？

查看试题解析
18. 已知：如图在菱形ABCD中，点E、F分别在边AB、AD上，BE＝DF，CE的延长线交DA的延长线于点G，CF的延长线交BA的延长线于点H.求证：△BEC∽△BCH.

查看试题解析
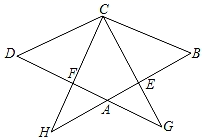19. 2020年庚子鼠年来临之际，一场来势汹汹的疫情，给我国带来了新的考验，疫情防控的人民战争在全国打响，举国上下团结奋斗、共克时艰，中国精神成为抗击病魔的利剑，是疫情防控战役中致胜的法宝，某医院为了鼓励工作人员抗击疫情，做如下活动：在一个不透明的盒子中装有4张分别标有A，B，C，D的卡片，A，B，C，D四张卡片的背面分别写有“防护、抗击、团结、奋斗”，它们的形状、大小完全相同，现随机从盒子中摸出两张卡片.

(1)、请用树状图或列表法表示摸出的两张卡片可能出现的所有结果；

(2)、求摸出的两张卡片中的词语能组成“团结奋斗”的概率.

查看试题解析
20. 如图，四边形ABCD中，BD垂直平分AC，垂足为点E，点F为四边形ABCD外一点，DA平分∠BDF，∠ADF＝∠BAD，且AF⊥AC.

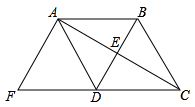(1)、求证：四边形ABDF是菱形；

(2)、若AB＝5，求AC的长.

查看试题解析
21. 某水果商场经销一种高档水果，原价每千克50元，连续两次降价后每千克32元，若每次下降的百分率相同．

(1)、求每次下降的百分率．

(2)、若每千克盈利10元，每天可售出500千克，经市场调查发现，在进货价不变的情况下商场决定采取适当的涨价措施，若每千克涨价1元，日销售量将减少20千克，现该商场要保证每天盈利6000元，且要尽快减少库存，那么每千克应涨价多少元?

(3)、若使商场每天的盈利达到最大值，则应涨价多少元?此时每天的最大盈利是多少?

查看试题解析
22. 在Rt△AEB中，∠AEB＝90°，以斜边AB为边向Rt△AEB外作正方形ABCD，正方形ABCD的对角线交于点O（如图1）.

(1)、如图1，OM⊥EM并交EB延长线于点M，ON⊥AE，且交EA于点N，求证：EO平分∠AEB；

(2)、如图1，延长EA到P，使AP＝BE，连接OP，试猜想线段OE与OP是否相等，并证明；

(3)、如图2，过点C作CF⊥EB并交EB的延长线于点F，过点D作DH⊥EA并交EA的延长线于点H，CF和DH的反向延长线交于点G，求证：四边形EFGH为正方形.

查看试题解析