陕西省宝鸡市岐山县2020-2021学年九年级上学期数学期中考试试卷
试卷更新日期:2021-09-07 类型:期中考试
一、单选题
-
1. 下列方程是关于x的一元二次方程的是( )A、 B、 C、 D、2. 同时抛掷两枚质地均匀的硬币,两个都是正面朝上的概率是( )A、 B、 C、 D、3. 用配方法解方程2x2-4x+1=0,则方程可变形为( )A、(x-2)2= B、2(x-2)2= C、(x-1)2= D、(2x-1)2=14. 如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
 A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形5. 定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )A、方有两个相等的实数根 B、方程有一根等于0 C、方程两根之和等于0 D、方程两根之积等于06. 九(1)班有2名升旗手,九(2)班、九(3)班各1名,若从4人中随机抽取2人担任下周的升旗手,则抽取的2人恰巧都来自九(1)班的概率是( )A、 B、 C、 D、7. 如图,任意四边形 中,点 分别是边 的中点,连接 ,对于四边形 的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形5. 定义:如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“和谐”方程;如果一元二次方程ax2+bx+c=0(a≠0)满足a﹣b+c=0那么我们称这个方程为“美好”方程,如果一个一元二次方程既是“和谐”方程又是“美好”方程,则下列结论正确的是( )A、方有两个相等的实数根 B、方程有一根等于0 C、方程两根之和等于0 D、方程两根之积等于06. 九(1)班有2名升旗手,九(2)班、九(3)班各1名,若从4人中随机抽取2人担任下周的升旗手,则抽取的2人恰巧都来自九(1)班的概率是( )A、 B、 C、 D、7. 如图,任意四边形 中,点 分别是边 的中点,连接 ,对于四边形 的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( ) A、若 ,则四边形 为菱形 B、若 ,则四边形 为矩形 C、若 ,且 ,则四边形 为正方形 D、若 与 互相平分,且 ,则四边形 是正方形8. 如图,在菱形 中, 于点H,则 的长为( )
A、若 ,则四边形 为菱形 B、若 ,则四边形 为矩形 C、若 ,且 ,则四边形 为正方形 D、若 与 互相平分,且 ,则四边形 是正方形8. 如图,在菱形 中, 于点H,则 的长为( ) A、1 B、 C、 D、9. 如图,有一块菱形纸片 ,沿高 剪下后拼成一个矩形,若矩形相邻两边 和 的长分别是5和3,则 的长是( )
A、1 B、 C、 D、9. 如图,有一块菱形纸片 ,沿高 剪下后拼成一个矩形,若矩形相邻两边 和 的长分别是5和3,则 的长是( ) A、 B、1 C、2 D、10. 扬帆中学有一块长 ,宽 的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为 ,则可列方程为( )
A、 B、1 C、2 D、10. 扬帆中学有一块长 ,宽 的矩形空地,计划在这块空地上划出四分之一的区域种花,小禹同学设计方案如图所示,求花带的宽度.设花带的宽度为 ,则可列方程为( )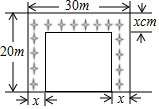 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 方程 的两个根分别为 ,则 的值为.12. 有一个转盘如图所示,转动该转盘两次,则指针两次都落在黄色区域的概率是.
 13. 如图,点E为正方形 对角线 上一点,且 ,则 的度数为.
13. 如图,点E为正方形 对角线 上一点,且 ,则 的度数为. 14. 如图,将一张矩形纸片 沿对角线 进行折叠,点C落在点 处,若 ,则重叠部分(阴影部分)的面积是(平方单位).
14. 如图,将一张矩形纸片 沿对角线 进行折叠,点C落在点 处,若 ,则重叠部分(阴影部分)的面积是(平方单位).
三、解答题
-
15. 用适当的方法解下列方程:(1)、 ;(2)、 .16. 如图, 是 的角平分线.
 (1)、尺规作图(不写作法,保留作图痕迹):作线段 的垂直平分线 ,分别交 于点 ,连接 ;(2)、判断四边形 的形状是.(直接写出答案)17. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF//BD交OE的延长线于点F,连接DF.
(1)、尺规作图(不写作法,保留作图痕迹):作线段 的垂直平分线 ,分别交 于点 ,连接 ;(2)、判断四边形 的形状是.(直接写出答案)17. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE.过点C作CF//BD交OE的延长线于点F,连接DF.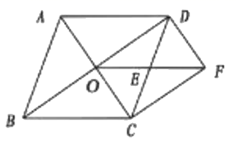
求证:
(1)、△ODE≌△FCE;(2)、四边形OCFD是矩形。18. 在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球试验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色后,再把它放回盒子中,不断重复上述过程,下表是试验中的组统计数据:摸球的次数m
100
200
300
500
800
1000
3000
摸到白球的次数n
66
128
171
302
481
599
1806
摸到白球的频率
0.66
0.64
0.57
0.604
0.601
0.599
0.602
(1)、若从盒子里随机摸出一球,则摸到白球的概率约为;(精确到0.1)(2)、估算盒子里约有白球个;(3)、若向盒子里再放入x个除颜色以外其它完全相同的球,这x个球中白球只有1个.然后每次将球搅拌均匀后,任意摸出一个球记下颜色后再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,请你推测x可能是多少?19. 书籍是人类宝贵的精神财富.读书则是传承优秀文化的通道.某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次.若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳进馆人次的能力不超过450人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.20. 为弘扬中华传统文化,某校举办了学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.元曲;D.论语.比赛形式分“单人组”和“双人组”.(1)、小明参加“单人组”,他从中随机抽取一个比赛项目,则抽到“唐诗”的是事件,其概率是;(2)、若小亮和小丽组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小亮和小丽都没有抽到“元曲”的概率是多少?请用画树状图或列表的方法进行说明.21. 如图, 中, , , ,点P从点A出发,以每秒 的速度沿 运动;同时点Q从点C出发,以每秒 的速度沿 运动,当Q到达点B时,点P同时停止运动.
求运动几秒时 的面积为 ?
