江西省赣州市十五县(市)十六校2020-2021学年度高二上学期文数期中联考试卷
试卷更新日期:2021-09-07 类型:期中考试
一、单选题
-
1. 直线 的倾斜角大小( )A、 B、 C、 D、2. 庚子新春,病毒肆虐,某老师为了解某班41名同学宅家学习期间上课、锻炼、休息等情况,决定将某班学生编号为01,02,…,41,利用下面的随机数表选取10个学生调查,选取方法是从随机数表第1行的第3列和第4列数字开始由左到右依次选取两个数字,则选出来的第4个学生的编号为( )
9258
0613
0604
7214
0702
4312
9728
0198
3104
9231
4935
8209
3624
4869
6938
7481
A、04 B、06 C、13 D、143. 已知直线 与直线 平行,则实数 ( )A、-3 B、3 C、-2 D、-2或34. 若两个变量 是线性相关的,且样本 的平均点为 ,则这组样本数据算得的线性回归方程不可能是( )A、 B、 C、 D、5. 已知圆 : ,该圆过点 的最短弦为 ,则弦 的直线方程为( )A、 B、 C、 D、6. 一组数据的平均数是26,方差是6,若将这组数据中的每一个数据都加上30,得到一组新数据,所得新数据的平均数和方差分别为( )A、56,6 B、30,6 C、56,10 D、30,107. 若 , 是两条不同的直线, , 是两个不同的平面, 则下列命题正确的是( )A、若 , , ,则 B、若 , ,则 C、若 , , , ,则 D、若 , ,则8. 某几何体的三视图如图所示,正视图和侧视图是腰长为2的等腰直角三角形,则该几何体的最长棱的长度为( ) A、2 B、 C、 D、49. 已知正方体 , 是 的中点,则异面直线 与 所成角的余弦值为( )
A、2 B、 C、 D、49. 已知正方体 , 是 的中点,则异面直线 与 所成角的余弦值为( )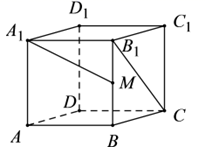 A、 B、 C、 D、10. 已知 , , , ,则执行如图所示的程序框图,输出的 值等于( )(结果用 , , , 表示)
A、 B、 C、 D、10. 已知 , , , ,则执行如图所示的程序框图,输出的 值等于( )(结果用 , , , 表示) A、 B、 C、 D、11. 已知圆 : ,直线 经过点 ,过直线 上的点 引圆 的两条切线,若切线长的最小值为2,则直线 的斜率 ( )A、 B、 C、-2或 D、 或12. 数学家阿波罗尼斯证明过这样一个命题:平面内到两定点距离之比为常数(常数大于零且不等于一)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系 中, ,动点 满足 ,得到动点 的轨迹是阿氏圆 .若对任意实数 ,直线 : 与圆 恒有公共点,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、11. 已知圆 : ,直线 经过点 ,过直线 上的点 引圆 的两条切线,若切线长的最小值为2,则直线 的斜率 ( )A、 B、 C、-2或 D、 或12. 数学家阿波罗尼斯证明过这样一个命题:平面内到两定点距离之比为常数(常数大于零且不等于一)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆,简称阿氏圆.已知在平面直角坐标系 中, ,动点 满足 ,得到动点 的轨迹是阿氏圆 .若对任意实数 ,直线 : 与圆 恒有公共点,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 已知 , ,若 ,则 .14. 已知 且 ,则 的最小值为.15. 某水平放置的平面图形的斜二测直观图是等腰梯形,它是底角为 ,腰和上底长均为1的等腰梯形,则该平面图形的周长为.16. 如图,平面四边形 中, , , , 为等边三角形,现将 沿 翻折,使点 移动至点 ,且 ,则三棱锥 的外接球的体积为.

三、解答题
-
17. 已知等比数列 各项均为正数, 是数列 的前 项和,且 , .(1)、求数列 的通项公式;(2)、设 ,求数列 的前 项和 .18. 在 中,角 , , 所对各边分别为 , , ,设向量 , 且满足 .(1)、求 ;(2)、若 , 的面积为3,求 的周长.19. 已知直三棱柱 中, , , 是 中点, 是 的中点.
 (1)、求证: ;(2)、求证: 平面 .20. 2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》, 此法典被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法.民法典与百姓生活密切相关,某学校有800名学生,为了解学生对民法典的认识程度,抽查了100名学生进行测试,并按学生的成绩(单位:分)制成如图所示频率分布直方图.
(1)、求证: ;(2)、求证: 平面 .20. 2020年5月28日,十三届全国人大三次会议表决通过了《中华人民共和国民法典》, 此法典被称为“社会生活的百科全书”,是新中国第一部以法典命名的法律,在法律体系中居于基础性地位,也是市场经济的基本法.民法典与百姓生活密切相关,某学校有800名学生,为了解学生对民法典的认识程度,抽查了100名学生进行测试,并按学生的成绩(单位:分)制成如图所示频率分布直方图. (1)、求 的值;(2)、若成绩在80分及以上视为优秀,根据样本数据估计该校学生对民法典认识程度优秀的人数;(3)、如果抽查的测试平均分超过75分,就表示该学校通过测试,试判断该校能否通过测试.
(1)、求 的值;(2)、若成绩在80分及以上视为优秀,根据样本数据估计该校学生对民法典认识程度优秀的人数;(3)、如果抽查的测试平均分超过75分,就表示该学校通过测试,试判断该校能否通过测试.
