山东省威海市乳山市2020-2021学年八级上学期数学期中试卷

试卷更新日期：2021-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下列从左到右的变形属于因式分解的是（）

A、x²-x-1=x（x-1）-1 B、a²- ab =a（a-b） C、x²-1= x（x- $\frac{1}{x}$ ） D、（x+2）（x-2）=x²-4

查看试题解析
2. 下列属于最简分式的是（）

A、 $\frac{{(1 - x)}^{2}}{x^{2} - 1}$ B、 $\frac{3 x}{x^{2} + 3}$ C、 $\frac{x + 1}{1 - x^{2}}$ D、 $\frac{17}{51 x}$

查看试题解析
3. 甲、乙、丙、丁四位同学五次数学测验成绩统计如右表所示，如果从这四位同学中，选出一位同学参加数学竞赛，那么应选___________去.

甲

乙

丙

丁

平均分

85

90

90

85

方差

50

42

50

42

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 将下列多项式分解因式，得到的结果中不含因式 $x - 1$ 的是（）

A、 $x^{2} - 1$ B、 $x (x - 2) + (2 - x)$ C、 $x^{2} + 2 x + 1$ D、 $x^{2} - 2 x + 1$

查看试题解析
5. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x的值为（）

A、0 B、1 C、﹣1 D、±1

查看试题解析
6. 下列各式：①﹣x²﹣y²；②﹣ $\frac{1}{4}$ a²b²+1； ③a²+ab+b²； ④﹣x²+2xy﹣y²；⑤ $\frac{1}{4}$ ﹣mn+m²n² ，用公式法分解因式的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 某校评选先进班集体，从“学习”、“卫生”、“纪律”、“活动参与”四个方面考核打分，各项满分均为100，八年级2班这四项得分依次为80，90，84，70，若按下表所占比例进行折分，则该班四项折分后的综合得分为（）

项目

学习

卫生

纪律

活动参与

所占比例

40%

25%

25%

10%

A、81.5 B、82.5 C、84 D、86

查看试题解析
8. 将下列分式中x，y(xy≠0)的值都扩大为原来的2倍后，分式的值一定不变的是（）

A、 $\frac{3 x + 1}{2 y}$ B、 $\frac{3 x}{2 y^{2}}$ C、 $\frac{3 x^{2}}{2 x y}$ D、 $\frac{3 x^{3}}{2 y^{2}}$

查看试题解析
9. “五一”江北水城文化旅游节期间，几名同学包租一辆面包车前去旅游，面包车的租价为180元，出发时又增加了两名同学，结果每名同学比原来少分摊3元车费.设原来参加游览的学生共x人.则所列方程是（）

A、 $\frac{180}{x - 2} - \frac{180}{x} = 3$ B、 $\frac{180}{x + 2} - \frac{180}{x} = 3$ C、 $\frac{180}{x} - \frac{180}{x - 2} = 3$ D、 $\frac{180}{x} - \frac{180}{x + 2} = 3$

查看试题解析
10. 已知关于x的分式方程 $\frac{x}{x - 2} - 4 = \frac{k}{2 - x}$ 的解为正数，则k的取值范围是（）

A、 $- 8 < k < 0$ B、 $k > - 8$ 且 $k \neq - 2$ C、 $k > - 8$ 且 $k \neq 2$ D、 $k < 4$ 且 $k \neq - 2$

查看试题解析

11. 刘老师对所在班级的全体学生进行实地家访，了解到每名学生家庭的有关信息，现从中随机抽取15名学生家庭的年收入情况，数据如下表：

年收入（单位：万元）	2	2.5	3	4	5	9	13
家庭个数	1	3	5	2	2	1	1

关于这15名学生家庭的年收入情况，下列说法错误的是（）

A、平均数是4万元 B、中位数是3万元 C、众数是3万元 D、极差是11万元

查看试题解析

12. “红色小讲解员”演讲比赛中，7位评委分别给出某位选手的原始评分.评定该选手成绩时，从7个原始评分中去掉一个最高分、一个最低分，得到5个有效评分.5个有效评分与7个原始评分相比，这两组数据一定不变的是（）.

A、中位数 B、众数 C、平均数 D、方差

查看试题解析

二、填空题

13. 因式分解：2m²﹣8n²= ．

查看试题解析
14. 一组数据1，0，2，a的唯一众数为1，则这组数据的方差是．

查看试题解析
15. 若关于 $x$ 的分式方程 $\frac{k - 1}{x - 2} - \frac{x}{x - 2} = 1$ 有增根，则 $k =$ ．

查看试题解析
16. 已知m²=3n+a ， n²=3m+a ， m≠n ，则m²+2mn+n²的值为．

查看试题解析
17. 化简： $(\frac{x^{2} + 4 x + 4}{x^{2} - 4} - x - 2) \div \frac{x + 2}{x - 2}$ ＝．

查看试题解析
18. 若x²﹣2x﹣5＝0，则x⁴﹣2x³+x²﹣12x﹣8的值为．

查看试题解析

三、解答题

19. 解分式方程： $1 - \frac{x - 2}{2 + x} = \frac{16}{x^{2} - 4}$

查看试题解析
20. 化简求值： $(\frac{x - 1}{x} - \frac{x - 2}{x + 1}) \div \frac{2 x^{2} - x}{x^{2} + 3 x + 2}$ ，其中x满足2x²﹣x﹣2＝0．

查看试题解析
21.

(1)、分解因式：（m﹣1）³﹣2（m﹣1）²+（m﹣1）；

(2)、利用分解因式计算：13（1﹣5²）（5⁴+1）（5⁸+1）（5¹⁶+1）．

查看试题解析

22. 每年的4月15日是我国全民国家安全教育日.某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生统计这部分学生的竞赛成绩(竞赛成绩均为整数，满分10分，6分及以上为合格).相关数据统计、整理如下：

八年级抽取的学生的竞赛成绩：4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10.

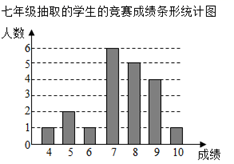
七，八年级抽取的学生的竞赛成绩统计表

年级	七年级	八年级
平均数	7.4	7.4
中位数	a	b
众数	7	c
合格率	85%	90%

根据以上信息，解答下列问题：

(1)、填空：a= ， b= ， c=.

(2)、估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；

(3)、比较样本数据，你认为哪个年级的成绩比较好？请说明理由（写出一条理由即可）；

查看试题解析

23. （阅读材料）把代数式通过配凑等手段，得到局部完全平方式，再进行有关运算和解题，这种解题方法叫做配方法．如：对于a²+6a+8．
⑴用配方法分解因式；

⑵当a取何值，代数式a²+6a+8有最小值？最小值是多少？

解：⑴原式＝a²+6a+8+1﹣1

＝a²+6a+9﹣1

＝（a+3）²﹣1

＝[（a+3）+1][（a+3）﹣1]

＝(a+4)(a+2)．

⑵对于（a+3）²﹣1，（a+3）²≥0．

所以，当a＝﹣3时，代数式a²+6a+8有最小值，最小值是﹣1．

（问题解决）利用配方法解决下列问题：

(1)、用配方法因式分解：x²+2x﹣3；

(2)、对于代数式 $\frac{1}{2 x^{2} - 8 x}$ ，有最大值还是最小值？并求出 $\frac{1}{2 x^{2} - 8 x}$ 的最大值或最小值．

查看试题解析
24. 中国是最早发现并利用茶的国家，形成了具有独特魅力的茶文化2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开．某茶店用4000元购进了A种茶叶若干盒，用8400元购进B种茶叶若干盒，所购B种茶叶比A种茶叶多10盒，且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍．

(1)、A ， B两种茶叶每盒进价分别为多少元？

(2)、第一次所购茶叶全部售完后第二次购进A ， B两种茶叶共100盒（进价不变），A种茶叶的售价是每盒300元，B种茶叶的售价是每盒400元．两种茶叶各售出一半后，为庆祝国际茶日，两种茶叶均打七折销售，全部售出后，第二次所购茶叶的利润为5800元（不考虑其他因素），求本次购进A ， B两种茶叶各多少盒？

查看试题解析
25. （阅读材料）
在进行计算或化简时，可以根据题目特点，将一个分数或分式变成两部分之差，如： $\frac{2}{3} = \frac{3 - 1}{3} = 1 - \frac{1}{3} ； \frac{1}{6} = \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3} ； \frac{1}{15} = \frac{1}{3 \times 5} = \frac{1}{2} (\frac{1}{3} - \frac{1}{5})$ 等．

（问题解决）

利用上述材料中的方法，解决下列问题：

(1)、求 $\frac{1}{2} + \frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \dots + \frac{1}{342} + \frac{1}{380}$ 的值；

(2)、求 $\frac{1}{4} + \frac{1}{12} + \frac{1}{24} + \frac{1}{40} + \dots + \frac{1}{2 (n - 1) n} + \frac{1}{2 n (n + 1)}$ 的值；

(3)、求 $\frac{1}{3} + \frac{1}{15} + \frac{1}{35} + \frac{1}{63} + \dots + \frac{1}{4 n^{2} - 1}$ 的值．

查看试题解析

项目	学习	卫生	纪律	活动参与
所占比例	40%	25%	25%	10%

	甲	乙	丙	丁
平均分	85	90	90	85
方差	50	42	50	42