山东省临沂市沂南县2020-2021学年八级上学期数学期中试卷

试卷更新日期：2021-09-07 类型：期中考试

进入出卷网下载

一、单选题

1. 下列三条线段，能组成三角形的是（）．

A、3，5，2 B、4，8，4 C、3，3，3 D、4，3，8

查看试题解析
2. 下列垃圾分类指引标志图形中，其中是轴对称图形的是（）．

A、 B、 C、 D、

查看试题解析
3. 下列图形中有稳定性的是（）

A、正方形 B、长方形 C、直角三角形 D、平行四边形

查看试题解析
4. 如图，在△ABC中，BC边上的高为（）

A、AD B、BE C、BF D、CG

查看试题解析
5. 一个多边形的每个内角均为140°，则这个多边形是（）

A、七边形 B、八边形 C、九边形 D、十边形

查看试题解析
6. 如图所示，若图中的两个三角形全等，则 $∠ α$ 度数是（）．

A、50° B、58° C、60° D、72°

查看试题解析
7. 如图所示，在△ABC中，∠C=90°，AD平分∠BAC ， DE⊥AB于E ， DE=4，BC=9，则BD的长为（）

A、6 B、5 C、4 D、3

查看试题解析
8. 如图，已知A ，D，B，E在同一条直线上，且AD = BE， AC = DF，补充下列其中一个条件后，不一定能得到△ABC≌△DEF 的是（）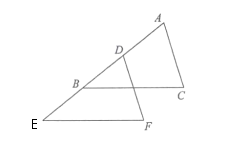

A、BC = EF B、AC//DF C、∠C = ∠F D、∠BAC = ∠EDF

查看试题解析
9. 如图，△ABC中，∠B=55°，∠C=30°，分别以点A和点C为圆心，大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点M，N作直线MN，交BC于点D，连结AD，则∠BAD的度数为（）

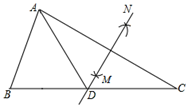A、65° B、60° C、55° D、45°

查看试题解析
10. 如图，欲测量内部无法到达的古塔相对两点A，B间的距离，可延长AO至C，使CO=AO，延长BO至D，使DO=BO，则△COD≌△AOB，从而通过测量CD就可测得A，B间的距离，其全等的根据是（）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
11. 如图， $Δ A B C$ 的面积为12， $A B = A C$ ， $B C = 4$ ， $A C$ 的垂直平分线 $E F$ 分别交 $A B$ ， $A C$ 边于点 $E$ ， $F$ ，若点 $D$ 为 $B C$ 边的中点，点 $P$ 为线段 $E F$ 上一动点，则 $Δ P C D$ 周长的最小值为（）

A、6 B、8 C、10 D、12

查看试题解析
12. 如图，在△ABC中，∠BAC＝90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G，交BE于点H，下面说法：①△ABE的面积＝△BCE的面积；②∠AFG＝∠AGF；③∠FAG＝2∠ACF；④BH＝CH．其中正确的是（）

A、①②③④ B、①②③ C、②④ D、①③

查看试题解析

二、填空题

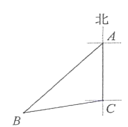
13. 在平面直角坐标系中，点 $A (- 3 ， - 2)$ 关于 $y$ 轴的对称点为．

查看试题解析
14. 如图，已知B处在A处的南偏西44°方向，C处在A处的正南方向，B处在C处的南偏西80°方向，则∠ABC的度数为

查看试题解析
15. 等腰三角形的周长为 $13 c m$ ，其中一边长为 $3 c m$ ，则该等腰三角形的底边长为 $c m$ .

查看试题解析
16. 如图，六边形ABCDEF内部有一点G，连结BG、DG. 若 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 + ∠ 5 = 440 °$ ，则∠BGD的大小为度.

查看试题解析
17. 如图，在等边 $△ A B C$ 中， $A B = 8$ ． $E$ 是 $B A$ 延长线上一点，且 $E A = 4$ ， $D$ 是 $B C$ 上一点，且 $D E = E C$ ，则 $B D$ 的长为．

查看试题解析
18. 在学习完“探索三角形全等的条件”一节后，小丽总结出很多全等三角形的模型，她设计了以下问题给同桌解决：做一个“ $U$ ”字形框架 $P A B Q ，$ 其中 $A B = 20 c m ， A P ， B Q$ 足够长， $P A ⊥ A B$ 于点 $A ， Q B ⊥ A B$ 于点 $B ，$ 点 $M$ 从 $B$ 出发向 $A$ 运动，点 $N$ 从 $B$ 出发向 $Q$ 运动，速度之比为 $2 ： 3 ，$ 运动到某一瞬间两点同时停止，在 $A P$ 上取点 $C ，$ 使 $△ A C M$ 与 $△ B M N$ 全等，则 $A C$ 的长度为 $c m .$

查看试题解析

三、解答题

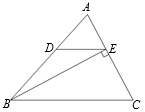
19. 如图，在△ABC中，BE是AC边上的高，DE∥BC，∠ADE＝48°，∠C＝62°，求∠ABE的度数.

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ， $B M$ 、 $C N$ 是 $△ A B C$ 两腰上的中线， $B M$ 与 $C N$ 相交于点 $O$ ．求证： $B M = C N$ ．

查看试题解析
21. 如图，在平面直角坐标系中，A（2，4），B（3，1），C（﹣2，﹣1）．

(1)、在图中作出△ABC关于x轴的对称图形△A₁B₁C₁ ，并写出点A₁ ， B₁ ， C₁的坐标；

(2)、求△ABC的面积．

查看试题解析
22. 如图，利用尺规，在 $△ ABC$ 的边 $AC$ 上方做 $∠ EAC ＝ ∠ ACB$ ，在射线 $AE$ 上截取 $AD ＝ BC$ ，连接 $CD$ ，并证明： $CD ∥ AB$ ．（尺规作图要求保留作图痕迹，不写作法）

查看试题解析
23. 如图，在等腰三角形 $△ A B C$ 中， $A C = B C$ ， $A C$ 边上的垂直平分线分别交 $A C$ ， $B C$ 于点 $D$ 和点 $E$ ，若 $∠ B A E = 45 °$ ．

(1)、求 $∠ C$ 的度数；

(2)、若 $D E = 2$ ，求 $A E$ 的长度．

查看试题解析
24. 如图，在 $△ A B C$ 中， $∠ A B C = ∠ A C B$ ， $B E = C F$ ， $E$ 为 $B C$ 边上一点，以 $E$ 为顶点作 $∠ A E F$ ， $∠ A E F$ 的一边交 $A C$ 于点 $F$ ，使 $∠ A E F = ∠ B$ ．请猜想 $A C$ 与 $E C$ 之间有怎样的数量关系，并说明理由．

查看试题解析
25. 如图，点 $O$ 是等边 $△ A B C$ 内一点， $∠ A O B = 110 °$ ， $∠ B O C = α$ ．以 $O C$ 为一边作等边三角形 $O C D$ ，连接 $A C$ 、 $A D$ ．

(1)、求证： $∠ O B C = ∠ D A C$ ；

(2)、求 $∠ O A D$ 的度数；

(3)、当 $α$ 为多少度时， $△ A O D$ 是等腰三角形？

查看试题解析