山东省聊城市2020-2021学年八级上学期数学期中试卷
试卷更新日期:2021-09-07 类型:期中考试
一、单选题
-
1. 下列防疫的图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,两个三角形是全等三角形,x的值是( )
2. 如图,两个三角形是全等三角形,x的值是( )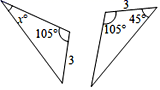 A、30° B、45° C、50° D、85°3. 如图,已知 ,以下条件不能证明 的是( )
A、30° B、45° C、50° D、85°3. 如图,已知 ,以下条件不能证明 的是( ) A、 B、 C、 D、4. 下列各式中的最简分式是( )A、 B、 C、 D、5. 如图,风筝的图案是以直线 为对称轴的轴对称图形,下列结论不一定成立的是( )
A、 B、 C、 D、4. 下列各式中的最简分式是( )A、 B、 C、 D、5. 如图,风筝的图案是以直线 为对称轴的轴对称图形,下列结论不一定成立的是( ) A、 垂直平分线段 B、 C、连接 、 ,其交点在 上 D、 ,6. 根据下列已知条件,能画出唯一的△ABC的是( )A、AB=3,BC=4,∠C=40° B、∠A=60°,∠B=45°,AB=4 C、∠C=90°,AB=6 D、AB=4,BC=3,∠A=30°7. 计算 的结果是( )A、 B、 C、 D、8. 如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数α是( )
A、 垂直平分线段 B、 C、连接 、 ,其交点在 上 D、 ,6. 根据下列已知条件,能画出唯一的△ABC的是( )A、AB=3,BC=4,∠C=40° B、∠A=60°,∠B=45°,AB=4 C、∠C=90°,AB=6 D、AB=4,BC=3,∠A=30°7. 计算 的结果是( )A、 B、 C、 D、8. 如图,将长方形纸片ABCD的角C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若FH平分∠BFE,则∠GFH的度数α是( )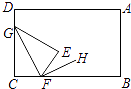 A、90°<α<180° B、0°<α<90° C、α=90° D、α随折痕GF位置的变化而变化9. 如图, 平分 , 于点 , , ,则 的面积等于( )
A、90°<α<180° B、0°<α<90° C、α=90° D、α随折痕GF位置的变化而变化9. 如图, 平分 , 于点 , , ,则 的面积等于( ) A、28 B、21 C、14 D、710. 如图,在△ABC中,∠C=63°,AD是BC边上的高,∠ABD=45°,点E在AC上,BE交AD于点F,DF=CD,则∠AFB的度数为( )
A、28 B、21 C、14 D、710. 如图,在△ABC中,∠C=63°,AD是BC边上的高,∠ABD=45°,点E在AC上,BE交AD于点F,DF=CD,则∠AFB的度数为( ) A、127° B、117° C、107° D、63°11. 如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( )
A、127° B、117° C、107° D、63°11. 如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有( ) A、8个 B、7个 C、6个 D、5个12. 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:
A、8个 B、7个 C、6个 D、5个12. 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )
 A、①②③ B、①③④ C、②③ D、①②③④
A、①②③ B、①③④ C、②③ D、①②③④二、填空题
-
13. 点M(-5,−2)关于x轴对称的点是点N,则点N的坐标是.14. 若分式 的值为0,则x的值为.15. 如图,△ABC≌△A'B'C,点B'在边AB上,线段A'B'与AC交于点D,若∠A=40°,∠B=60°,则∠A'CB的度数为 .
 16. 有一等腰钝角三角形纸片,若能从一个顶点出发,将其剪成两个等腰三角形纸片,则等腰钝角三角形纸片的顶角度数为 .17. 已知,在长方形ABCD中,AB=6,AD=10,延长BC至E,使CE=4,连接DE,动点F从B出发,以每秒2个单位长度的速度沿BC﹣CD﹣DA向终点A运动,设点F的运动时间为t秒,当t的值为时,△ABF和△DCE全等.
16. 有一等腰钝角三角形纸片,若能从一个顶点出发,将其剪成两个等腰三角形纸片,则等腰钝角三角形纸片的顶角度数为 .17. 已知,在长方形ABCD中,AB=6,AD=10,延长BC至E,使CE=4,连接DE,动点F从B出发,以每秒2个单位长度的速度沿BC﹣CD﹣DA向终点A运动,设点F的运动时间为t秒,当t的值为时,△ABF和△DCE全等.
三、解答题
-
18. 约分(1)、 ;(2)、 ;(3)、 .19. 计算(1)、 ;(2)、 ;(3)、 .20. 如图,网格中的 与 为轴对称图形,且顶点都在格点上.
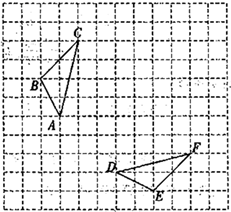 (1)、利用网格,作出 与 的对称轴l;(2)、结合图形,在对称轴l上画出一点 ,使得 最小;(3)、如果每个小正方形的边长为1,请直接写出 的面积.21. 已知:如图,AB∥ED,点F、点C在AD上,AB=DE,AF=DC.求证:BC=EF.
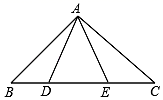
(1)、利用网格,作出 与 的对称轴l;(2)、结合图形,在对称轴l上画出一点 ,使得 最小;(3)、如果每个小正方形的边长为1,请直接写出 的面积.21. 已知:如图,AB∥ED,点F、点C在AD上,AB=DE,AF=DC.求证:BC=EF.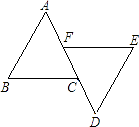 22. 如图,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.
22. 如图,已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E. (1)、求∠BAD的度数;
(1)、求∠BAD的度数;
(2)、若AB=10,BC=12,求△ABD的周长.23. 如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,那么BD与CE相等吗?为什么?