山东省济南市长清区2020-2021学年八级上学期数学期中试卷
试卷更新日期:2021-09-07 类型:期中考试
一、单选题
-
1. 9的算术平方根是( )A、3 B、-3 C、±3 D、812. 下列实数中的无理数是( )A、0.7 B、 C、 D、3. 平面直角坐标系中,点P(3,-4)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 以下列各组数为线段长,不能构成直角三角形的一组是( )A、1,2, B、3,4,5 C、1, ,2 D、6,8,125. 函数 的图象一定经过点( )A、 B、 C、 D、6. 点 关于 轴的对称点 的坐标是( )A、 B、 C、 D、7. 下列各式中,正确的是( )A、 B、 C、 D、8. 正比例函数 ( )的函数值y随x的增大而减小,则一次函数 的图象大致是( )A、
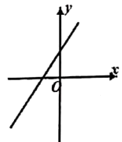 B、
B、 C、
C、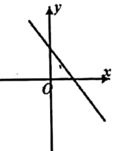 D、
D、 9. 点 、 在直线 上,若 ,则 与 大小关系是( )
9. 点 、 在直线 上,若 ,则 与 大小关系是( )
A、 B、 C、 D、无法确定10. 如图, 中, , , ,将 折叠,使 点与 的中点 重合,折痕为 ,则线段 的长为( ) A、5 B、4 C、 D、11. 甲乙两人同时沿着一条笔直的公路朝同一方向前行,开始时,乙在甲前2千米处,甲、乙两人行走的路程 (千米)与时间 (时)的函数图象如图所示,下列说法正确的是( )
A、5 B、4 C、 D、11. 甲乙两人同时沿着一条笔直的公路朝同一方向前行,开始时,乙在甲前2千米处,甲、乙两人行走的路程 (千米)与时间 (时)的函数图象如图所示,下列说法正确的是( )①乙的速度为4千米/时②经过1小时,甲追上乙;③经过0.5小时,乙行走的路程约为2千米;④经过1.5小时,乙在甲的前面.
 A、①②③ B、①② C、②③ D、②12. 如图,平面直角坐标系中,已知点 , , , ,动点 从点 出发,以每秒2个单位的速度按逆时针方向沿四边形 的边做环绕运动;另一动点 从点 出发,以每秒3个单位的速度按顺时针方向沿四边形 的边做环绕运动,则第2020次相遇点的坐标是( )
A、①②③ B、①② C、②③ D、②12. 如图,平面直角坐标系中,已知点 , , , ,动点 从点 出发,以每秒2个单位的速度按逆时针方向沿四边形 的边做环绕运动;另一动点 从点 出发,以每秒3个单位的速度按顺时针方向沿四边形 的边做环绕运动,则第2020次相遇点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 化简 .14. 如果 在 轴上,那么点 的坐标是 .15. 若 ,则 的立方根是 .16. 如图,将直线OA向上平移2个单位长度,则平移后的直线的表达式为。
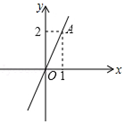 17. 如图所示的圆柱体中底面圆的半径是 ,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是 . (结果保留根号)
17. 如图所示的圆柱体中底面圆的半径是 ,高为3,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是 . (结果保留根号) 18. 在平面直角坐标系中,等边 的位置如图,若 ,则点 的坐标为 .
18. 在平面直角坐标系中,等边 的位置如图,若 ,则点 的坐标为 .
三、解答题
-
19. 计算:(1)、(2)、20. 计算:(1)、(2)、21. 已知一次函数 的图象经过点 、 两点.
 (1)、画出这个函数的图象;(2)、当 时, .22. 如图,一个梯子 长25米,顶端 靠在墙 上(墙与地面垂直),这时梯子下端 与墙角 距离为7米.
(1)、画出这个函数的图象;(2)、当 时, .22. 如图,一个梯子 长25米,顶端 靠在墙 上(墙与地面垂直),这时梯子下端 与墙角 距离为7米. (1)、求梯子顶端 与地面的距离 的长;(2)、若梯子的顶端 下滑到 ,使 ,求梯子的下端 滑动的距离 的长.23. 如图,四边形ABCD各顶点的坐标分别是A(0,0),B(8,0),C(6,4),D(3,6),求出四边形ABCD的面积.
(1)、求梯子顶端 与地面的距离 的长;(2)、若梯子的顶端 下滑到 ,使 ,求梯子的下端 滑动的距离 的长.23. 如图,四边形ABCD各顶点的坐标分别是A(0,0),B(8,0),C(6,4),D(3,6),求出四边形ABCD的面积. 24. 如图, 的三个顶点的坐标分别为 , , .
24. 如图, 的三个顶点的坐标分别为 , , . (1)、在图中作出 关于 轴的对称图形 ;(2)、请直接写出点 关于 轴的对称点 的坐标:;(3)、在 轴上找一点 ,使得 周长最小,并求出 周长的最小值.25. 如图,一次函数 的图象与 轴、 轴分别相交于 , 两点,点 的坐标为 , ,其中 是直线 上的一个动点.
(1)、在图中作出 关于 轴的对称图形 ;(2)、请直接写出点 关于 轴的对称点 的坐标:;(3)、在 轴上找一点 ,使得 周长最小,并求出 周长的最小值.25. 如图,一次函数 的图象与 轴、 轴分别相交于 , 两点,点 的坐标为 , ,其中 是直线 上的一个动点. (1)、求 与 的值;(2)、若 的面积为6,求点 的坐标.26. 某单位急需用车,但又不准备买车,他们准备和一个个体车主或一个出租车公司其中的一家签定月租车合同,设汽车每月行驶 千米,应付给个体车主的月费用是 元,应付给出租车公司的月租费用是 元, , 分别与 之间的函数关系图象如图,观察图象回答下列问题:
(1)、求 与 的值;(2)、若 的面积为6,求点 的坐标.26. 某单位急需用车,但又不准备买车,他们准备和一个个体车主或一个出租车公司其中的一家签定月租车合同,设汽车每月行驶 千米,应付给个体车主的月费用是 元,应付给出租车公司的月租费用是 元, , 分别与 之间的函数关系图象如图,观察图象回答下列问题: (1)、求 , 分别与 之间的函数关系式;(2)、每月行驶的路程等于多少时,租两家的费用相同?(3)、如果这个单位估计每月行驶的路程为2400千米,那么这个单位租哪一家的车合算,并说明理由?27. 如图,在平面直角坐标系中, 为坐标原点,四边形 是长方形,点 、 的坐标分别为 , ,点 是 的中点,点 为线段 上的点.
(1)、求 , 分别与 之间的函数关系式;(2)、每月行驶的路程等于多少时,租两家的费用相同?(3)、如果这个单位估计每月行驶的路程为2400千米,那么这个单位租哪一家的车合算,并说明理由?27. 如图,在平面直角坐标系中, 为坐标原点,四边形 是长方形,点 、 的坐标分别为 , ,点 是 的中点,点 为线段 上的点. (1)、请写出 、 两点的坐标;(2)、若点 的坐标为 ,
(1)、请写出 、 两点的坐标;(2)、若点 的坐标为 ,①求过点 、 两点的直线解析式;
②小明发现 ,请利用所学知识说明理由;
③小明在继续探究这个题的过程中发现,此时 是一个等腰三角形,那么小明的问题来了,在线段 上还存在不存在其它 点使得 还是一个等腰三角形,若不存在请说明理由;若存在,请直接写出符合要求的点的坐标.